题目内容
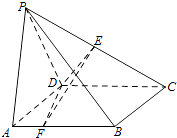
【题目】如图，在四棱锥P﹣ABCD中，底面ABCD是正方形，AD=PD=2，PA=2 
，∠PDC=120°，点E为线段PC的中点，点F在线段AB上． （Ⅰ）若AF= 
，求证：CD⊥EF；
（Ⅱ）设平面DEF与平面DPA所成二面角的平面角为θ，试确定点F的位置，使得cosθ= 
．
【答案】证明：（Ⅰ）在△PCD中，PD=CD=2， ∵E为PC的中点，∴DE平分∠PDC，∠PDE=60°，
∴在Rt△PDE中，DE=PDcos60°=1，
过E作EH⊥CD于H，则 
，连结FH，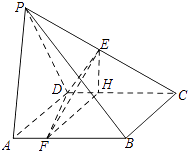
∵ 
，∴四边形AFHD是矩形，
∴CD⊥FH，又CD⊥EH，FH∩EH=H，∴CD⊥平面EFH，
又EF平面EFH，∴CD⊥EF．
解：（Ⅱ）∵AD=PD=2， 
，∴AD⊥PD，又AD⊥DC，
∴AD⊥平面PCD，
又AD平面ABCD，∴平面PCD⊥平面ABCD．
过D作DG⊥DC交PC于点G，则由平面PCD⊥平面ABCD知，DG⊥平面ABCD，
故DA，DC，DG两两垂直，以D为原点，以DA，DC，DG所在直线分别为x，y，z轴，
建立如图所示空间直角坐标系O﹣xyz，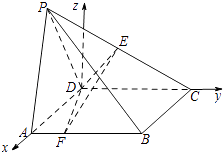 
则A（2，0，0），B（2，2，0），C（0，2，0）， 
，
又知E为PC的中点，E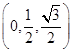 
，设F（2，t，0），
则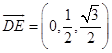 
， 
， 
， 
．
设平面DEF的法向量为 
=（x1 ， y1 ， z1），
则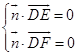 
，∴ 
，
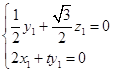取z1=﹣2，得平面DEF的一个法向量 
，
设平面ADP的法向量为 =（x2 ， y2 ， z2），
则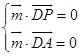 
，∴ 
，
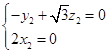取z2=1，得 
．
∴ 
，解得 
，
∴当 
时，满足 
．
【解析】（Ⅰ）过E作EH⊥CD于H，连结FH，推导出四边形AFHD是矩形，由此能证明CD⊥EF．（Ⅱ）过D作DG⊥DC交PC于点G，以D为原点，以DA，DC，DG所在直线分别为x，y，z轴，建立空间直角坐标系O﹣xz，利用向量法能求出当 
时，满足 
．
【考点精析】认真审题，首先需要了解空间中直线与直线之间的位置关系(相交直线：同一平面内，有且只有一个公共点；平行直线：同一平面内，没有公共点；异面直线： 不同在任何一个平面内，没有公共点)．
