Question

【题目】如图，在长方体中，点是棱的中点，点 在棱上，且（为实数）．

（1）求二面角的余弦值；

（2）当时，求直线与平面所成角的正弦值的大小；

（3）求证：直线与直线不可能垂直．

Answer 1

【答案】（1）；（2）；（3）见解析.

【解析】分析：(1)建立如图所示的空间直角坐标系，写出相应点的坐标，算出相应向量的坐标，利用垂直向量的数量积等于零的方法建立方程组，算出平面对应的法向量，之后应用平面的法向量所成角的余弦值求得二面角的余弦值；’

(2)当时，可得E,F的坐标，从而求得的坐标，进而算出的余弦值，再由其为锐角，结合直线与平面所成角的定义，即可算出直线与平面所成角的正弦值的大小；

(3)假设直线与直线垂直，根据向量的数量积等于零，建立关于的等量关系式，化简可得，由根的判别式小于零得该方程无解，从而得到假设不成立，从而得到原结论成立.

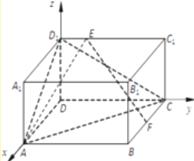
详解：（1）如图所示，建立空间直角坐标系．

则 ，

设平面的法向量为，

则．即．令，则．

∴平面的一个法向量．又平面的一个法向量为．

故，即二面角的余弦值为.

（2）当λ =时，E（0，1，2），F（1，4，0），．

所以．

因为 ，所以为锐角，

从而直线EF与平面所成角的正弦值的大小为．

(3)假设，则．

∵，

∴，．

∴．化简得．

该方程无解，所以假设不成立，即直线不可能与直线不可能垂直．