Question

如图，内外两个椭圆的离心率相同，从外层椭圆顶点向内层椭圆引切线AC，BD，设内层椭圆方程为 ，若直线AC与BD的斜率之积为，则椭圆的离心率为（  ）

A．

B．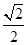

C．

D．

Answer 1

C

试题分析：【方法一】由于内层椭圆和外层椭圆的离心率相等，不妨设外层椭圆的方程为，设切线的方程为，则，
消去得，
由，
化简得，
同理可得，，
因此，所以，因此，
故椭圆的离心率为.故选C.
【方法二】椭圆在其上一点处的切点方程为，
设，，由于内外两个椭圆的离心率相同，则可设外层椭圆的方程为，则，内层椭圆在点C处的切线方程为，而AC的方程为，其斜率为，同理直线BD的方程为，其斜率为，
∴  ①，
直线AC过点，则有，
直线BD过点，则有，∴，
∴，∴，设，，
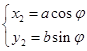不妨设点C为第一象限内的点，则点D为第二象限内的点，则为锐角，为钝角，
则，∴，则为锐角，∴，
∴，∴，由①式得，
，∴，
∴，∴，∴，故选C.