题目内容
过椭圆 右焦点且斜率为1的直线被椭圆截得的弦MN的长为( )
右焦点且斜率为1的直线被椭圆截得的弦MN的长为( )
 右焦点且斜率为1的直线被椭圆截得的弦MN的长为( )
右焦点且斜率为1的直线被椭圆截得的弦MN的长为( )A.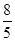 | B. | C. | D. |
A
试题分析:求出过椭圆
 右焦点且斜率为1的直线方程,代入椭圆
右焦点且斜率为1的直线方程,代入椭圆 ,可得一元二次方程,利用弦长公式,即可求弦MN的长.
,可得一元二次方程,利用弦长公式,即可求弦MN的长.
练习册系列答案
相关题目
题目内容
 右焦点且斜率为1的直线被椭圆截得的弦MN的长为( )
右焦点且斜率为1的直线被椭圆截得的弦MN的长为( )A.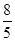 | B. | C. | D. |
 右焦点且斜率为1的直线方程,代入椭圆
右焦点且斜率为1的直线方程,代入椭圆 ,可得一元二次方程,利用弦长公式,即可求弦MN的长.
,可得一元二次方程,利用弦长公式,即可求弦MN的长.