题目内容
斜率为1的直线l与椭圆 +y2=1交于不同两点A,B,则|AB|的最大值为( )
+y2=1交于不同两点A,B,则|AB|的最大值为( )
 +y2=1交于不同两点A,B,则|AB|的最大值为( )
+y2=1交于不同两点A,B,则|AB|的最大值为( )| A.2 | B. |
C. | D. |
C
设直线l的方程为y=x+t,代入 +y2=1,消去y,得
+y2=1,消去y,得 x2+2tx+t2-1=0,由题意得Δ=(2t)2-5(t2-1)>0,即t2<5,
x2+2tx+t2-1=0,由题意得Δ=(2t)2-5(t2-1)>0,即t2<5,
弦长|AB|=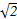 ·
·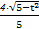 ≤
≤ .
.
 +y2=1,消去y,得
+y2=1,消去y,得 x2+2tx+t2-1=0,由题意得Δ=(2t)2-5(t2-1)>0,即t2<5,
x2+2tx+t2-1=0,由题意得Δ=(2t)2-5(t2-1)>0,即t2<5,弦长|AB|=
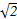 ·
·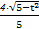 ≤
≤ .
.
练习册系列答案
 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案
相关题目
 |=|
|=| |?若存在,求出D点的坐标;若不存在,说明理由.
|?若存在,求出D点的坐标;若不存在,说明理由.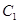 的中心为原点
的中心为原点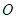 ,离心率
,离心率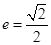 ,其一个焦点在抛物线
,其一个焦点在抛物线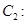
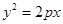 的准线上,若抛物线
的准线上,若抛物线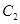 与直线
与直线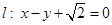 相切.
相切.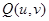 在椭圆
在椭圆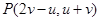 的运动轨迹为
的运动轨迹为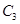 .若点
.若点 满足:
满足: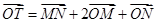 ,其中
,其中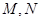 是
是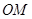 与
与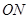 的斜率之积为
的斜率之积为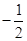 ,试说明:是否存在两个定点
,试说明:是否存在两个定点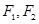 ,使得
,使得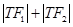 为定值?若存在,求
为定值?若存在,求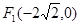 和
和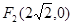 ,长轴长为6,设直线
,长轴长为6,设直线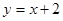 交椭圆C于A、B两点,求线段AB的中点坐标
交椭圆C于A、B两点,求线段AB的中点坐标 是方程
是方程 表示椭圆或双曲线的 ( )
表示椭圆或双曲线的 ( ) +
+ =1(a>b>0)的两个焦点,P为椭圆C上一点,且
=1(a>b>0)的两个焦点,P为椭圆C上一点,且 ⊥
⊥ ,若△PF1F2的面积为9,则b= .
,若△PF1F2的面积为9,则b= . ,若直线AC与BD的斜率之积为
,若直线AC与BD的斜率之积为 ,则椭圆的离心率为( )
,则椭圆的离心率为( )

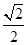


 +
+ =1
=1 +
+ =1
=1 +
+ =1
=1 +
+ =1
=1