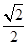题目内容
已知椭圆C: +
+ =1(a>b>0)的一个顶点为A(2,0),离心率为
=1(a>b>0)的一个顶点为A(2,0),离心率为 .直线y=k(x-1)与椭圆C交于不同的两点M,N.
.直线y=k(x-1)与椭圆C交于不同的两点M,N.
(1)求椭圆C的方程;
(2)当△AMN的面积为 时,求k的值.
时,求k的值.
 +
+ =1(a>b>0)的一个顶点为A(2,0),离心率为
=1(a>b>0)的一个顶点为A(2,0),离心率为 .直线y=k(x-1)与椭圆C交于不同的两点M,N.
.直线y=k(x-1)与椭圆C交于不同的两点M,N.(1)求椭圆C的方程;
(2)当△AMN的面积为
 时,求k的值.
时,求k的值.(1) 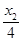 +
+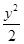 =1 (2) k=±1
=1 (2) k=±1
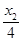 +
+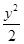 =1 (2) k=±1
=1 (2) k=±1解:(1)由题设知,椭圆焦点在x轴上,
∴a=2.
由e=
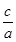 =
= 得c=
得c=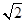 ,
,∴b2=a2-c2=2.
∴椭圆C的方程为
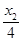 +
+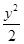 =1.
=1.(2)由
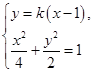 消去y,
消去y,整理得(1+2k2)x2-4k2x+2k2-4=0.
设M(x1,y1),N(x2,y2).
则Δ=(-4k2)2-4(1+2k2)(2k2-4)>0(※)
且x1+x2=
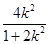 ,x1·x2=
,x1·x2=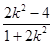 ,
,∴|MN|=
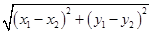
=
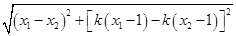
=
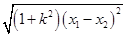
=
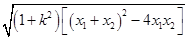
=
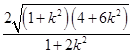
设点A(2,0)到直线y=k(x-1)的距离为d,
则d=
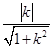 .
.∴S△AMN=
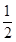 |MN|·d=
|MN|·d=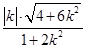 =
= ,
,解得k=±1,
代入(※)式成立,∴k=±1.

练习册系列答案
相关题目
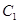 的中心为原点
的中心为原点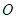 ,离心率
,离心率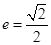 ,其一个焦点在抛物线
,其一个焦点在抛物线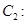
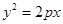 的准线上,若抛物线
的准线上,若抛物线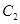 与直线
与直线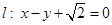 相切.
相切.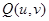 在椭圆
在椭圆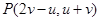 的运动轨迹为
的运动轨迹为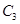 .若点
.若点 满足:
满足: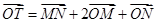 ,其中
,其中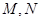 是
是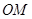 与
与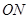 的斜率之积为
的斜率之积为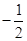 ,试说明:是否存在两个定点
,试说明:是否存在两个定点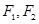 ,使得
,使得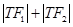 为定值?若存在,求
为定值?若存在,求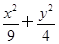 =1的焦点为F1、F2,点P为椭圆上的动点,当∠F1PF2为钝角时,求点P的横坐标x0的取值范围.
=1的焦点为F1、F2,点P为椭圆上的动点,当∠F1PF2为钝角时,求点P的横坐标x0的取值范围. 是方程
是方程 表示椭圆或双曲线的 ( )
表示椭圆或双曲线的 ( )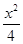 +y2=1与双曲线C2的公共焦点,A,B分别是C1,C2在第二、四象限的公共点.若四边形AF1BF2为矩形,则C2的离心率是( )
+y2=1与双曲线C2的公共焦点,A,B分别是C1,C2在第二、四象限的公共点.若四边形AF1BF2为矩形,则C2的离心率是( )




 +
+ =1上有两个动点P、Q,E(3,0),EP⊥EQ,则
=1上有两个动点P、Q,E(3,0),EP⊥EQ,则 ·
· 的最小值为( )
的最小值为( )
 +
+ =1(a>b>0)的两个焦点,P为椭圆C上一点,且
=1(a>b>0)的两个焦点,P为椭圆C上一点,且 ⊥
⊥ ,若△PF1F2的面积为9,则b= .
,若△PF1F2的面积为9,则b= . ,若直线AC与BD的斜率之积为
,若直线AC与BD的斜率之积为 ,则椭圆的离心率为( )
,则椭圆的离心率为( )

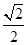


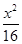 +
+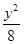 =1的离心率为( )
=1的离心率为( )