Question

【题目】如图，三棱柱中，侧棱平面，为等腰直角三角形，，且分别是的中点．

（Ⅰ）求证：平面；

（Ⅱ）求锐二面角的余弦值．

Answer 1

【答案】（Ⅰ）见解析；（Ⅱ）；

【解析】

试题分析：（1）要证明平面，需证明及，前面在平面中证明，利用勾股定理，即通过计算设，则.∴，∴.后者通过线面垂直与线线垂直的转化得，即由面面，得面，再得。（2）求二面角的余弦值，可通过作、证、算，本题可过作,则为所求二面角的平面角.也可利用空间向量求，先建系，求出平面及平面的法向量，利用向量数量积求出两法向量的夹角，最后根据二面角与向量夹角关系得出结论.

试题解析：（1）连结，∵是等腰直角三角形斜边的中点，∴.

又三棱柱为直三棱柱，

∴面面，

∴面，. 2分

设，则.

∴，∴. 4分

又，∴平面. 6分

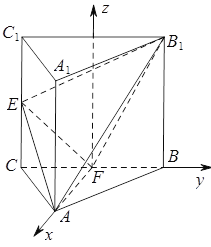
（2）以为坐标原点，分别为轴建立直角坐标系如图，设，

则，

，. 8分

由（1）知，平面，

∴可取平面的法向量.

设平面的法向量为，

由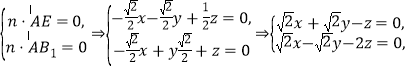

∴可取. 10分

设锐二面角的大小为，

则.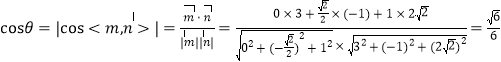

∴所求锐二面角的余弦值为. 12分