��Ŀ����
����Ŀ����ͼ����������OABC�У�OΪ����ԭ�㣬��A������Ϊ��10��0������C������Ϊ��0��10�����ֱ��߶�OA��ABʮ�ȷ֣��ֵ�ֱ��ΪA1 �� A2 �� ����A9��B1 �� B2 �� ����B9 �� ����OBi �� ��Ai��x��Ĵ�����OBi �� ���ڵ� ![]() ��
�� 
��1����֤���� ![]() ����ͬһ���������ϣ�����������E�ķ��̣�
����ͬһ���������ϣ�����������E�ķ��̣�
��2������C��ֱ��l��������E���ڲ�ͬ������M��N������OCM���OCN�����֮��Ϊ4��1����ֱ��l�ķ��̣�
���𰸡�
��1��֤���������⣬�� ![]() ����x�ᴹֱ��ֱ�߷���Ϊx=i��Bi������Ϊ��10��i����
����x�ᴹֱ��ֱ�߷���Ϊx=i��Bi������Ϊ��10��i����
��ֱ��OBi�ķ���Ϊ ![]() ��
��
��Pi��x��y������ 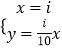 �����
����� ![]() ����x2=10y��
����x2=10y��
��� ![]() ����ͬһ���������ϣ�������E�ķ���Ϊx2=10y��
����ͬһ���������ϣ�������E�ķ���Ϊx2=10y��
��2���⣺�����⣬��ֱ��l�ķ���Ϊy=kx+10��
���� ![]() ��ȥy�õ�x2��10kx��100=0��
��ȥy�õ�x2��10kx��100=0��
��ʱ����0��ֱ���������ߺ���������ͬ�Ľ��㣬
��ΪM��x1��y1����N��x2��y2������x1+x2=10k��x1x2=��100��
��S��OCM=4S��OCN����|x1|=4|x2|����x1=��4x2��
���� 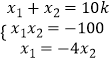 �����
����� ![]() ��
��
��ֱ��l�ķ���Ϊ ![]() ����Ϊ3x+2y��20=0��3x��2y+20=0��
����Ϊ3x+2y��20=0��3x��2y+20=0��
����������1�������⣬����� ![]() ����x�ᴹֱ��ֱ�߷���Ϊx=i��Bi������Ϊ��10��i�������ɵõ�ֱ��OBi�ķ���Ϊ
����x�ᴹֱ��ֱ�߷���Ϊx=i��Bi������Ϊ��10��i�������ɵõ�ֱ��OBi�ķ���Ϊ ![]() ����������
���������� 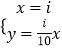 �����ɵõ�Pi����ķ��̣���2�������⣬��ֱ��l�ķ���Ϊy=kx+10���������ߵķ��������õ�һԪ���η��̣����ø���ϵ���Ĺ�ϵ�������������ʽS��OCM=S��OCN �� �ɵ�|x1|=4|x2|����x1=��4x2 �� �������ɵõ�k�������õ�ֱ�߷��̣�
�����ɵõ�Pi����ķ��̣���2�������⣬��ֱ��l�ķ���Ϊy=kx+10���������ߵķ��������õ�һԪ���η��̣����ø���ϵ���Ĺ�ϵ�������������ʽS��OCM=S��OCN �� �ɵ�|x1|=4|x2|����x1=��4x2 �� �������ɵõ�k�������õ�ֱ�߷��̣�

 һŵ��ҵ�����ҵ���ּ�����������������ϵ�д�
һŵ��ҵ�����ҵ���ּ�����������������ϵ�д�


