题目内容
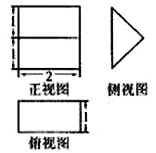
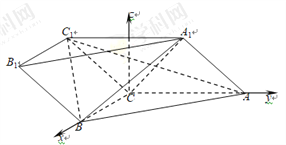
【题目】如图,在三棱柱![]() 中,
中, ![]() ,平面
,平面![]() 平面
平面![]() .
.

(1)求证: ![]() ;
;
(2)若![]() ,求
,求![]() .
.

【答案】(1)见解析;(2)![]()
【解析】试题分析:(1)第(1)问,通过证明C1C⊥平面A1BC得到CC1⊥A1B. (2)第(2)问,以C为坐标原点,分别以![]() 的方向为x轴,y轴的正方向建立空间直角坐标系,利用空间向量求二面角A1-BC1-A的余弦值 .
的方向为x轴,y轴的正方向建立空间直角坐标系,利用空间向量求二面角A1-BC1-A的余弦值 .
试题解析:
(1)因为平面AA1C1C⊥平面ABC,交线为AC,又BC⊥AC,
所以BC⊥平面AA1C1C,
因为C1C![]() 平面AA1C1C,
平面AA1C1C,
从而有BC⊥C1C.
因为∠A1CC1=90°,所以A1C⊥C1C,
又因为BC∩A1C=C,
所以C1C⊥平面A1BC,
A1B![]() 平面A1BC,所以CC1⊥A1B.
平面A1BC,所以CC1⊥A1B.
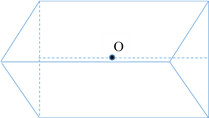
(2)如图,以C为坐标原点,分别以![]() 的方向为x轴,y轴的正方向建立空间直角坐标系C-xyz.
的方向为x轴,y轴的正方向建立空间直角坐标系C-xyz.
由∠A1CC1=90°,AC=![]() AA1得A1C=AA1.
AA1得A1C=AA1.
不妨设BC=AC=![]() AA1=2,
AA1=2,
则B(2,0,0),C1(0,-1,1),A(0,2,0),A1(0,1,1),
所以![]() =(0,-2,0),
=(0,-2,0), ![]() =(-2,-1,1),
=(-2,-1,1), ![]() =(2,-2,0),
=(2,-2,0),
设平面A1BC1的一个法向量为![]() ,
,
由![]() ·
·![]() =0,
=0, ![]() ·
·![]() =0,可取
=0,可取![]() =(1,0,2).
=(1,0,2).
设平面ABC1的一个法向量为![]() ,
,
由![]() ·
·![]() =0,
=0, ![]() ·
·![]() =0,可取
=0,可取![]() =(1,1,3).
=(1,1,3).
cos![]() ,
, ![]() =
=![]() =
=![]() ,
,
又因为二面角A1-BC1-A为锐二面角,
所以二面角A1-BC1-A的余弦值为![]() .
.

 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案【题目】假设有一套住房的房价从2002年的20万元上涨到2012年的40万元,下表给出了两种价格增长方式,其中![]() 是按直线上升的房价,
是按直线上升的房价,![]() 是按指数增长的房价,t是2002年以来经过的年数.
是按指数增长的房价,t是2002年以来经过的年数.
t | 0 | 5 | 10 | 15 | 20 |
| 20 | 30 | 40 | 50 | 60 |
| 20 |
| 40 |
| 80 |
(1)求函数![]() 的解析式;
的解析式;
(2)求函数![]() 的解析式;
的解析式;
(3)完成上表空格中的数据,并在同一直角坐标系中画出两个函数的图象,然后比较两种价格增长方式的差异.