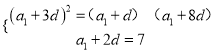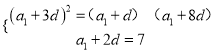题目内容
【题目】已知椭圆![]() :
: ![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
, ![]() ,且离心率为
,且离心率为![]() ,
, ![]() 为椭圆上任意一点,当
为椭圆上任意一点,当![]() 时,
时, ![]() 的面积为1.
的面积为1.
(1)求椭圆![]() 的方程;
的方程;
(2)已知点![]() 是椭圆
是椭圆![]() 上异于椭圆顶点的一点,延长直线
上异于椭圆顶点的一点,延长直线![]() ,
, ![]() 分别与椭圆交于点
分别与椭圆交于点![]() ,
, ![]() ,设直线
,设直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,求证:
,求证: ![]() 为定值.
为定值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:(1)设![]() 由题
由题 ,由此求出
,由此求出![]() ,可得椭圆
,可得椭圆![]() 的方程;
的方程;
(2)设![]() ,
, ![]() ,
,
当直线![]() 的斜率不存在时,可得
的斜率不存在时,可得![]() ;
;
当直线![]() 的斜率不存在时,同理可得
的斜率不存在时,同理可得![]() .
.
当直线![]() 、
、![]() 的斜率存在时,
的斜率存在时,![]() ,
,
设直线![]() 的方程为
的方程为![]() ,则由
,则由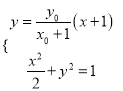 消去
消去![]() 通过运算可得
通过运算可得
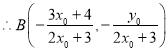 ,同理可得
,同理可得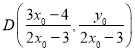 ,由此得到直线
,由此得到直线![]() 的斜率为
的斜率为![]() ,
,
![]() 直线
直线![]() 的斜率为
的斜率为![]() ,进而可得
,进而可得![]() .
.
试题解析:(1)设![]() 由题
由题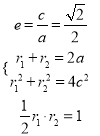 ,
,
解得![]() ,则
,则![]() ,
,
![]() 椭圆
椭圆![]() 的方程为
的方程为![]() .
.
(2)设![]() ,
, ![]() ,
,
当直线![]() 的斜率不存在时,设
的斜率不存在时,设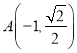 ,则
,则 ,
,
直线![]() 的方程为
的方程为![]() 代入
代入![]() ,可得
,可得![]() ,
,
![]() ,
, ![]() ,则
,则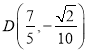 ,
,
![]() 直线
直线![]() 的斜率为
的斜率为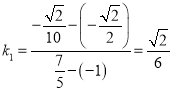 ,直线
,直线![]() 的斜率为
的斜率为![]() ,
,
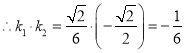 ,
,
当直线![]() 的斜率不存在时,同理可得
的斜率不存在时,同理可得![]() .
.
当直线![]() 、
、![]() 的斜率存在时,
的斜率存在时,![]() ,
,
设直线![]() 的方程为
的方程为![]() ,则由
,则由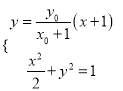 消去
消去![]() 可得:
可得:
![]() ,
,
又![]() ,则
,则![]() ,代入上述方程可得
,代入上述方程可得
![]() ,
,
![]() ,则
,则![]()
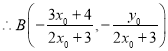 ,
,
设直线![]() 的方程为
的方程为![]() ,同理可得
,同理可得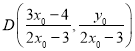 ,
,
![]() 直线
直线![]() 的斜率为
的斜率为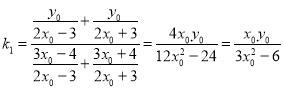 ,
,
![]() 直线
直线![]() 的斜率为
的斜率为![]() ,
,
![]()
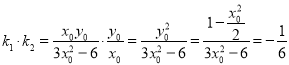 .
.
所以,直线![]() 与
与![]() 的斜率之积为定值
的斜率之积为定值![]() ,即
,即![]() .
.
【题型】解答题
【结束】
21
【题目】已知函数![]() ,
, ![]() ,在
,在![]() 处的切线方程为
处的切线方程为![]() .
.
(1)求![]() ,
, ![]() ;
;
(2)若方程![]() 有两个实数根
有两个实数根![]() ,
, ![]() ,且
,且![]() ,证明:
,证明: ![]() .
.
【答案】(1)![]() ,
, ![]() ;(2)见解析
;(2)见解析
【解析】试题分析: ![]() 在
在![]() 处的切线方程为
处的切线方程为![]() ,求导算出切线方程即可求出结果
,求导算出切线方程即可求出结果![]() 构造
构造![]() ,求导,得
,求导,得![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增,设
上单调递增,设![]() 的根为
的根为![]() ,证得
,证得![]() ,讨论证得
,讨论证得![]() 的根为
的根为![]() ,
, ![]() ,从而得证结论
,从而得证结论
解析:(1)由题意![]() ,所以
,所以![]() ,
,
又![]() ,所以
,所以![]() ,
,
若![]() ,则
,则![]() ,与
,与![]() 矛盾,故
矛盾,故![]() ,
, ![]() .
.
(2)由(Ⅰ)可知![]() ,
, ![]() ,
,
设![]() 在(-1,0)处的切线方程为
在(-1,0)处的切线方程为![]() ,
,
易得, ![]() ,令
,令![]()
即![]() ,
, ![]() ,
,
当![]() 时,
时, ![]()
当![]() 时,
时,
设![]() ,
, ![]() ,
,
故函数![]() 在
在![]() 上单调递增,又
上单调递增,又![]() ,
,
所以当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() ,
,
所以函数![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增,
上单调递增,
故![]() ,
, ![]() ,
,
设![]() 的根为
的根为![]() ,则
,则![]() ,
,
又函数![]() 单调递减,故
单调递减,故![]() ,故
,故![]() ,
,
设![]() 在(0,0)处的切线方程为
在(0,0)处的切线方程为![]() ,易得
,易得![]() ,
,
令![]() ,
, ![]() ,
,
当![]() 时,
时, ![]() ,
,
当![]() 时,
时,
![]()
故函数![]() 在
在![]() 上单调递增,又
上单调递增,又![]() ,
,
所以当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() ,
,
所以函数![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增,
上单调递增,
![]() ,
, ![]() ,
,
设![]() 的根为
的根为![]() ,则
,则![]() ,
,
又函数![]() 单调递增,故
单调递增,故![]() ,故
,故![]() ,
,
又![]() ,
,
![]() .
.

 阅读快车系列答案
阅读快车系列答案