题目内容
【题目】已知向量 ![]() ,其中
,其中![]() .函数
.函数![]() 的图象过点
的图象过点![]() ,点
,点![]() 与其相邻的最高点的距离为4.
与其相邻的最高点的距离为4.
(Ⅰ)求函数![]() 的单调递减区间;
的单调递减区间;
(Ⅱ)计算![]() 的值;
的值;
(Ⅲ)设函数![]() ,试讨论函数
,试讨论函数![]() 在区间 [0,3] 上的零点个数.
在区间 [0,3] 上的零点个数.
【答案】(Ⅰ)![]() ,
,![]() ;(Ⅱ)2018;(Ⅲ)详见解析.
;(Ⅱ)2018;(Ⅲ)详见解析.
【解析】
(Ⅰ)由数量积的坐标运算可得f(x),由题意求得ω![]() ,再由函数f(x)的图象过点B(1,2)列式求得
,再由函数f(x)的图象过点B(1,2)列式求得![]() .则函数解析式可求,由复合函数的单调性求得f(x)的单调递增区间;
.则函数解析式可求,由复合函数的单调性求得f(x)的单调递增区间;
(Ⅱ)由(Ⅰ)知,f(x)=1+sin![]() ,可得f(x)是周期为4的周期函数,且f(1)=2,f(2)=1,f(3)=0,f(4)=1.得到f(1)+f(2)+f(3)+f(4)=4.
,可得f(x)是周期为4的周期函数,且f(1)=2,f(2)=1,f(3)=0,f(4)=1.得到f(1)+f(2)+f(3)+f(4)=4.
进一步可得结论;
(Ⅲ)g(x)=f(x)﹣m﹣1![]() ,函数g(x)在[0,3]上的零点个数,即为函数y=sin
,函数g(x)在[0,3]上的零点个数,即为函数y=sin![]() 的图象与直线y=m在[0,3]上的交点个数.数形结合得答案.
的图象与直线y=m在[0,3]上的交点个数.数形结合得答案.
(Ⅰ)∵![]() (
(![]() ,
,![]() cos2(ωx+φ)),
cos2(ωx+φ)),![]() (
(![]() ,
,![]() ),
),
∴f(x)![]() cos2(ωx+
cos2(ωx+![]() )=1﹣cos2(ωx+
)=1﹣cos2(ωx+![]() )),
)),
∴f(x)max=2,则点B(1,2)为函数f(x)的图象的一个最高点.
∵点B与其相邻的最高点的距离为4,∴![]() ,得ω
,得ω![]() .
.
∵函数f(x)的图象过点B(1,2),∴![]() ,即sin2φ=1.
,即sin2φ=1.
∵0<![]() ,∴
,∴![]() .
.
∴f(x)=1﹣cos2(![]() )=1+sin
)=1+sin![]() ,
,
由![]() ,得
,得![]() ,
,![]() .
.
![]() 的单调递减区间是
的单调递减区间是![]() ,
,![]() .
.
(Ⅱ)由(Ⅰ)知,f(x)=1+sin![]() ,
,
∴f(x)是周期为4的周期函数,且f(1)=2,f(2)=1,f(3)=0,f(4)=1.
∴f(1)+f(2)+f(3)+f(4)=4.
而2017=4×504+1,
∴f(1)+f(2)+…+f(2017)=4×504+2=2018;
(Ⅲ)g(x)=f(x)﹣m﹣1![]() ,函数g(x)在[0,3]上的零点个数,
,函数g(x)在[0,3]上的零点个数,
即为函数y=sin![]() 的图象与直线y=m在[0,3]上的交点个数.
的图象与直线y=m在[0,3]上的交点个数.
在同一直角坐标系内作出两个函数的图象如图:
①当m>1或m<﹣1时,两函数的图象在[0,3]内无公共点;
②当﹣1≤m<0或m=1时,两函数的图象在[0,3]内有一个共点;
③当0≤m<1时,两函数的图象在[0,3]内有两个共点.
综上,当m>1或m<﹣1时,函数g(x)在[0,3]上无零点;
②当﹣1≤m<0或m=1时,函数g(x)在[0,3]内有1个零点;
③当0≤m<1时,函数g(x)在[0,3]内有2个零点.
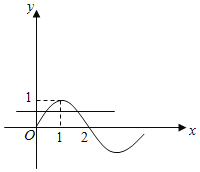

【题目】某企业生产一种产品,质量测试分为:指标不小于![]() 为一等品;指标不小于
为一等品;指标不小于![]() 且小于
且小于![]() 为二等品;指标小于
为二等品;指标小于![]() 为三等品。其中每件一等品可盈利
为三等品。其中每件一等品可盈利![]() 元,每件二等品可盈利
元,每件二等品可盈利![]() 元,每件三等品亏损
元,每件三等品亏损![]() 元。现对学徒甲和正式工人乙生产的产品各
元。现对学徒甲和正式工人乙生产的产品各![]() 件的检测结果统计如下:
件的检测结果统计如下:
测试指标 |
|
|
|
|
|
|
甲 |
|
|
|
|
|
|
乙 |
|
|
|
|
|
|
根据上表统计得到甲、乙生产产品等级的频率分别估计为他们生产产品等级的概率。求:
(1)乙生产一件产品,盈利不小于![]() 元的概率;
元的概率;
(2)若甲、乙一天生产产品分别为![]() 件和
件和![]() 件,估计甲、乙两人一天共为企业创收多少元?
件,估计甲、乙两人一天共为企业创收多少元?
(3)从甲测试指标为![]() 与乙测试指标为
与乙测试指标为![]() 共
共![]() 件产品中选取
件产品中选取![]() 件,求两件产品的测试指标差的绝对值大于
件,求两件产品的测试指标差的绝对值大于![]() 的概率.
的概率.
【题目】某个产品有若干零部件构成,加工时需要经过7道工序,分别记为![]() .其中,有些工序因为是制造不同的零部件,所以可以在几台机器上同时加工;有些工序因为是对同一个零部件进行处理,所以存在加工顺序关系,若加工工序
.其中,有些工序因为是制造不同的零部件,所以可以在几台机器上同时加工;有些工序因为是对同一个零部件进行处理,所以存在加工顺序关系,若加工工序![]() 必须要在工序
必须要在工序![]() 完成后才能开工,则称
完成后才能开工,则称![]() 为
为![]() 的紧前工序.现将各工序的加工次序及所需时间(单位:小时)列表如下:
的紧前工序.现将各工序的加工次序及所需时间(单位:小时)列表如下:
工序 |
|
|
|
|
|
|
|
加工时间 | 3 | 4 | 2 | 2 | 2 | 1 | 5 |
紧前工序 | 无 |
| 无 |
|
|
|
|
现有两台性能相同的生产机器同时加工该产品,则完成该产品的最短加工时间是( )
(假定每道工序只能安排在一台机器上,且不能间断.)
A. 11个小时 B. 10个小时 C. 9个小时 D. 8个小时
