题目内容
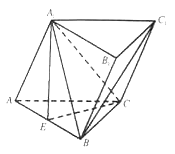
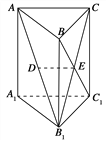
【题目】如图,在直三棱柱ABC-A1B1C1中,已知AC⊥BC,BC=CC1,设AB1的中点为D,B1C∩BC1=E.

求证:(1)DE∥平面AA1C1C;
(2)BC1⊥AB1.
【答案】(1)详见解析;(2)详见解析.
【解析】
试题分析:(1) 由题意知,E为B1C的中点,又D为AB1的中点,因此DE∥AC,根据线面平行的判定定理得证;(2)由CC1⊥平面ABC,可得AC⊥CC1,又因为AC⊥BC,由线面垂直的判定定理可得AC⊥平面BCC1B1,进而可得B1C⊥AC,又BC1⊥B1C,证得BC1⊥平面B1AC,故命题成立.
试题解析:
(1)由题意知,E为B1C的中点,
又D为AB1的中点,因此DE∥AC.
又因为DE平面AA1C1C,AC平面AA1C1C,
所以DE∥平面AA1C1C.
(2)因为棱柱ABC-A1B1C1是直三棱柱,
所以CC1⊥平面ABC.
因为AC平面ABC,所以AC⊥CC1.
又因为AC⊥BC,CC1平面BCC1B1,
BC平面BCC1B1,BC∩CC1=C,
所以AC⊥平面BCC1B1,
又因为BC1平面BCC1B1,所以B1C⊥AC.
因为BC=CC1,所以矩形BCC1B1是正方形,因此BC1⊥B1C.
因为AC,B1C平面B1AC,AC∩B1C=C,所以BC1⊥平面B1AC.
又因为AB1平面B1AC,所以BC1⊥AB1.

练习册系列答案
相关题目