Question

【题目】已知函数f（x）=﹣x3+ax2+bx+c图象上的点P（1，﹣2）处的切线方程为y=﹣3x+1．
（1）若函数f（x）在x=﹣2时有极值，求f（x）的表达式
（2）若函数f（x）在区间[﹣2，0]上单调递增，求实数b的取值范围．

Answer 1

【答案】
（1）解：f′（x）=﹣3x2+2ax+b，

因为函数f（x）在x=1处的切线斜率为﹣3，

所以f′（1）=﹣3+2a+b=﹣3，即2a+b=0，

又f（1）=﹣1+a+b+c=﹣2得a+b+c=﹣1．

函数f（x）在x=﹣2时有极值，所以f'（﹣2）=﹣12﹣4a+b=0，

解得a=﹣2，b=4，c=﹣3，

所以f（x）=﹣x3﹣2x2+4x﹣3

（2）解：因为函数f（x）在区间[﹣2，0]上单调递增，所以导函数f′（x）=﹣3x2﹣bx+b

在区间[﹣2，0]上的值恒大于或等于零，

则 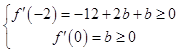得b≥4，所以实数b的取值范围为[4，+∞）.

【解析】（1）对函数f（x）求导，由题意点P（1，﹣2）处的切线方程为y=﹣3x+1，可得f′（1）=﹣3，再根据f（1）=﹣1，又由f′（﹣2）=0联立方程求出a，b，c，从而求出f（x）的表达式．（2）由题意函数f（x）在区间[﹣2，0]上单调递增，对其求导可得f′（x）在区间[﹣2，0]大于或等于0，从而求出b的范围．