Question

【题目】已知函数为二次函数，不等式的解集，且在区间上的最大值为12.

（1）求函数的解析式；

（2）设函数在上的最小值为，求的表达式及的最小值.

Answer 1

【答案】(1)

（2）

.

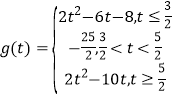
【解析】

（1）不等式的解集，得出f（x）=m（x﹣5）x，m＞0，f（x）在区间[﹣1，3]上的最大值为12．f（﹣1）=12，即可求出解析式．

（2）根据二次函数的对称轴和单调性判断．

（1）∵f（x）是二次函数，不等式f（x）＜0的解集为（0，5），

∴f（x）=m（x﹣5）x，m＞0，对称轴x=，

∵f（x）在区间[﹣1，3]上的最大值为12，

∴f（﹣1）=12，

∴m=2，

∴f（x）=2x2﹣10x，

（2）由（1）知，f（x）=2x2﹣10x，

对称轴是x=，t≥时，f（x）在[t，t+1]递增，

故f（x）min=f（t）=2t2﹣10t，

t＜＜t+1即＜t＜时，f（x）min=f（）=﹣，

t+1≤即t≤时，f（x）min=f（t+1）=2t2﹣6t﹣8，

综上，，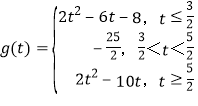

则．