题目内容
【题目】已知函数 ![]() .
.
(Ⅰ)求f(x)的单调递减区间;
(Ⅱ)设α是锐角,且 ![]() ,求f(α)的值.
,求f(α)的值.
【答案】解:(Ⅰ) ![]() =
= ![]() cos2x﹣
cos2x﹣ ![]() sin2x=
sin2x= ![]() cos2x. 由 2kπ≤2x≤2kπ+π,k∈z,可得 kπ≤x≤kπ+
cos2x. 由 2kπ≤2x≤2kπ+π,k∈z,可得 kπ≤x≤kπ+ ![]() ,故求f(x)的单调递减区间为[kπ,kπ+
,故求f(x)的单调递减区间为[kπ,kπ+ ![]() ],k∈z.
],k∈z.
(Ⅱ)∵α是锐角,且 ![]() ,∴
,∴ ![]() =
= ![]() ,α=
,α= ![]() .
.
∴f(α)= ![]() cos2x=
cos2x= ![]() cos
cos ![]() =
= 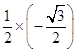 =﹣
=﹣ ![]()
【解析】(Ⅰ) ![]() =
= ![]() cos2x,由 2kπ≤2x≤2kπ+π,k∈z,求得f(x)的单调递减区间.(Ⅱ)由 α是锐角,且
cos2x,由 2kπ≤2x≤2kπ+π,k∈z,求得f(x)的单调递减区间.(Ⅱ)由 α是锐角,且 ![]() ,得
,得 ![]() =
= ![]() ,α=
,α= ![]() ,故 f(α)=
,故 f(α)= ![]() cos2x=
cos2x= ![]() cos
cos ![]() .
.
【考点精析】本题主要考查了两角和与差的正弦公式和正弦函数的单调性的相关知识点,需要掌握两角和与差的正弦公式:![]() ;正弦函数的单调性:在
;正弦函数的单调性:在![]()
![]() 上是增函数;在
上是增函数;在![]()
![]() 上是减函数才能正确解答此题.
上是减函数才能正确解答此题.

练习册系列答案
相关题目
【题目】为了解少年儿童的肥胖是否与常喝碳酸饮料有关,现对30名六年级学生进行了问卷调查得到如下列联表:平均每天喝500ml以上为常喝,体重超过50kg为肥胖。
常喝 | 不常喝 | 合计 | |
肥胖 | 6 | 2 | 8 |
不肥胖 | 4 | 18 | 22 |
合计 | 10 | 20 | 30 |
已知在全部30人中随机抽取1人,抽到肥胖的学生的概率为![]() 。
。
(1)是否有![]() 的把握认为肥胖与常喝碳酸饮料有关?说明你的理由
的把握认为肥胖与常喝碳酸饮料有关?说明你的理由
(2)现从常喝碳酸饮料且肥胖的学生中(2名女生),抽取2人参加电视节目,则正好抽到一男一女的概率是多少?
参考数据:

(参考公式:![]() ,其中
,其中![]() )
)