题目内容
15.圆x2+y2=16的切线与x轴、y轴的正半轴分别交于A、B两点,则|AB|最小值为8.分析 设直线的方程为bx+ay-ab=0,由直线和圆相切可得a2b2=16(a2+b2),由基本不等式可得$\sqrt{{a}^{2}+{b}^{2}}$的最小值,即得答案.
解答 解:由题意设直线的方程为:$\frac{x}{a}$+$\frac{y}{b}$=1,即bx+ay-ab=0,
∵圆心(0,0)到的距离为半径4,
∴$\frac{|ab|}{\sqrt{{b}^{2}+{a}^{2}}}$=4,平方整理可得a2b2=16(a2+b2),
由基本不等式可得16(a2+b2)=a2b2≤($\frac{{a}^{2}+{b}^{2}}{2}$)2,
∴解不等式可得|AB|=$\sqrt{{a}^{2}+{b}^{2}}$≥8,
当且仅当a=b=4$\sqrt{2}$时等号成立,
故答案为:8.
点评 本题考查圆的切线,涉及点到直线的距离公式和基本不等式求最值,属中档题.

练习册系列答案
相关题目
5.长方体ABCD-A1B1C1D1中,若$\overrightarrow{AB}$=3i,$\overrightarrow{AD}$=2j,$\overrightarrow{A{A}_{1}}$=5k,则$\overrightarrow{A{C}_{1}}$=( )
| A. | $\overrightarrow{i}$+$\overrightarrow{j}$+$\overrightarrow{k}$ | B. | $\frac{1}{3}$$\overrightarrow{i}$+$\frac{1}{2}$$\overrightarrow{j}$+$\frac{1}{5}$$\overrightarrow{k}$ | C. | 3$\overrightarrow{i}$+2$\overrightarrow{j}$+5$\overrightarrow{k}$ | D. | 3$\overrightarrow{i}$+2$\overrightarrow{j}$-5$\overrightarrow{k}$ |
4.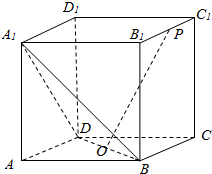 如图,在正方体ABCD-A1B1C1D1中,点O为线段BD的中点.设点P在线段B1C1上,直线OP与平面A1BD所成的角为α,则sinα的取值范围是( )
如图,在正方体ABCD-A1B1C1D1中,点O为线段BD的中点.设点P在线段B1C1上,直线OP与平面A1BD所成的角为α,则sinα的取值范围是( )
 如图,在正方体ABCD-A1B1C1D1中,点O为线段BD的中点.设点P在线段B1C1上,直线OP与平面A1BD所成的角为α,则sinα的取值范围是( )
如图,在正方体ABCD-A1B1C1D1中,点O为线段BD的中点.设点P在线段B1C1上,直线OP与平面A1BD所成的角为α,则sinα的取值范围是( )| A. | $[\frac{{\sqrt{6}}}{3},1]$ | B. | $[\frac{{\sqrt{2}}}{3},1]$ | C. | $[\frac{{\sqrt{2}}}{3},\frac{{2\sqrt{2}}}{3}]$ | D. | $[\frac{{\sqrt{6}}}{3},\frac{{2\sqrt{2}}}{3}]$ |