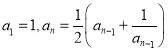题目内容
【题目】选修4-5:不等式选讲
已知函数![]() ,
,![]() .
.
(1)当![]() 时,解关于
时,解关于![]() 的不等式
的不等式![]() ;
;
(2)若对任意![]() ,都存在
,都存在![]() ,使得不等式
,使得不等式![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1) ![]() .
.
(2) ![]() .
.
【解析】分析:第一问首先将![]() 代入
代入![]() ,然后根据零点分段将绝对值符号去掉,再去解对应的各段上的不等式,从而求得
,然后根据零点分段将绝对值符号去掉,再去解对应的各段上的不等式,从而求得![]() 的范围,最后求并集得到结果;第二问根据所给的量词,将恒成立问题转化为相应的最值问题,结合三角不等式,分类讨论,求得结果.
的范围,最后求并集得到结果;第二问根据所给的量词,将恒成立问题转化为相应的最值问题,结合三角不等式,分类讨论,求得结果.
详解:(1)当![]() 时,
时,![]() ,则
,则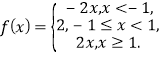
当![]() 时,由
时,由![]() 得,
得,![]() ,解得
,解得![]() ;
;
当![]() 时,
时,![]() 恒成立;
恒成立;
当![]() 时,由
时,由![]() 得,
得,![]() ,解得
,解得![]() .
.
所以![]() 的解集为
的解集为![]() .
.
(2)因为对任意![]() ,都存在
,都存在![]() ,使得不等式
,使得不等式![]() 成立,
成立,
所以![]() .
.
因为![]() ,所以
,所以![]() ,
,
且![]() ,…①
,…①
当![]() 时,①式等号成立,即
时,①式等号成立,即![]() .
.
又因为![]() ,…②
,…②
当![]() 时,②式等号成立,即
时,②式等号成立,即![]() .
.
所以![]() ,整理得,
,整理得,![]() ,
,
解得![]() 或
或![]() ,即
,即![]() 的取值范围为
的取值范围为![]() .
.

练习册系列答案
相关题目