题目内容
【题目】为弘扬民族古典文化,市电视台举行古诗词知识竞赛,某轮比赛由节目主持人随机从题库中抽取题目让选手抢答,回答正确将给该选手记正10分,否则记负10分.根据以往统计,某参赛选手能答对每一个问题的概率均为![]() ;现记“该选手在回答完
;现记“该选手在回答完![]() 个问题后的总得分为
个问题后的总得分为![]() ”.
”.
(1)求![]() 且
且![]() (
(![]() )的概率;
)的概率;
(2)记![]() ,求
,求![]() 的分布列,并计算数学期望
的分布列,并计算数学期望![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题本题属于独立重复试验问题,求概率的关键是发生的次数![]() ,(1)
,(1)![]() ,说明回答
,说明回答![]() 个问题后,正确
个问题后,正确![]() 个,错误
个,错误![]() 个.要满足
个.要满足![]() ,则第一题回答正确,第2题如果正确,则后面4题2对2错,第2题如果错误,则第3题正确,后面3题2对1错,由此可计算出概率;(2)由
,则第一题回答正确,第2题如果正确,则后面4题2对2错,第2题如果错误,则第3题正确,后面3题2对1错,由此可计算出概率;(2)由![]() 可知
可知![]() 的取值为
的取值为![]() .按概率公式计算概率可得分布列,可计算出数学期望.
.按概率公式计算概率可得分布列,可计算出数学期望.
试题解析:(1)当![]() 时,即回答
时,即回答![]() 个问题后,正确
个问题后,正确![]() 个,错误
个,错误![]() 个. 若回答正确
个. 若回答正确![]() 个和第
个和第![]() 个问题,则其余
个问题,则其余![]() 个问题可任意回答正确
个问题可任意回答正确![]() 个问题;若第一个问题回答正确,第
个问题;若第一个问题回答正确,第![]() 个问题回答错误,第三个问题回答正确,则其余三个问题可任意回答正确
个问题回答错误,第三个问题回答正确,则其余三个问题可任意回答正确![]() 个.
个.
故所求概率为:![]() .
.
(2)由![]() 可知
可知![]() 的取值为
的取值为![]() .
.
![]() ,
,![]() .
.
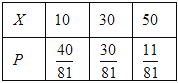
故![]() 的分布列为:
的分布列为:
![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

