题目内容
【题目】f(x)是定义在(0,+∞)上的单调增函数,满足f(xy)=f(x)+f(y),f(3)=1,当f(x)+f(x-8)≤2时,x的取值范围是( )
A.(8,+∞)B.(8,9]C.[8,9]D.(0,8)
【答案】B
【解析】
令x=y=3,利用f(3)=1即可求得f(9)=2,由f(x)+f(x﹣8)≤2得f[x(x﹣8)]≤f(9),再由单调性得到不等式组,解之即可.
∵f(3)=1,
∴f(9)=f(3×3)=f(3)+f(3)=2;
∵函数f(x)是定义在(0,+∞)上的增函数,
f(xy)=f(x)+f(y),f(9)=2,
∴f(x)+f(x﹣8)≤2f[x(x﹣8)]≤f(9),
∴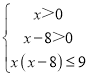 ,
,
解得:8<x≤9.
∴原不等式的解集为:(8,9].
故选:B.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目