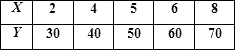
题目内容
【题目】已知抛物线的方程为![]() :
: ![]() ,过点
,过点![]() 的一条直线与抛物线
的一条直线与抛物线![]() 交于
交于![]() 两点,若抛物线在
两点,若抛物线在![]() 两点的切线交于点
两点的切线交于点![]() .
.
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)设直线![]() 的斜率存在,取为
的斜率存在,取为![]() ,取直线
,取直线![]() 的斜率为
的斜率为![]() ,请验证
,请验证![]() 是否为定值?若是,计算出该值;若不是,请说明理由.
是否为定值?若是,计算出该值;若不是,请说明理由.
【答案】(Ⅰ)![]() ,
, ![]() (Ⅱ)-2为定值.
(Ⅱ)-2为定值.
【解析】(Ⅰ)由AB直线与抛物线交于两点可知,直线AB不与x轴垂直,故可设![]() ,代入
,代入![]() ,
,
整理得: ![]() ,方程①的判别式
,方程①的判别式![]() ,故
,故![]() 时均满足题目要求.
时均满足题目要求.
记交点坐标为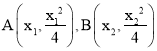 ,则
,则![]() 为方程①的两根,
为方程①的两根,
故由韦达定理可知, ![]() .
.
将抛物线方程转化为![]() ,则
,则![]() ,故A点处的切线方程为
,故A点处的切线方程为![]() ,
,
整理得![]() ,
,
同理可得,B点处的切线方程为![]() ,记两条切线的交点
,记两条切线的交点![]() ,
,
联立两条切线的方程,解得点![]() 坐标为
坐标为![]() ,
,
故点P的轨迹方程为![]() ,
, ![]()
(Ⅱ)当![]() 时,
时, ![]() ,此时直线PQ即为y轴,与直线AB的夹角为
,此时直线PQ即为y轴,与直线AB的夹角为![]() .
.
当![]() 时,记直线PQ的斜率
时,记直线PQ的斜率![]() ,又由于直线AB的斜率为
,又由于直线AB的斜率为![]() ,
,
![]() 为定值.
为定值.

练习册系列答案
相关题目
【题目】雾霾天气是一种大气污染状态,PM2.5被认为是造成雾霾天气的“元凶”,PM2.5日均值越小,空气质量越好.国家环境标准设定的PM2.5日均值(微克/立方米)与空气质量等级对应关系如表:
PM2.5日均值 | 0﹣﹣35 | 35﹣﹣75 | 75﹣﹣115 | 115﹣﹣150 | 150﹣﹣250 | 250以上 |
空气质量等级 | 1级 | 2级 | 3级 | 4级 | 5级 | 6级 |
由某市城市环境监测网获得4月份某5天甲、乙两城市的空气质量指数数据,用茎叶图表示,如图所示.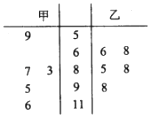
(1)试根据统计数据,分别写出两城区的PM2.5日均值的中位数,并从中位数角度判断哪个城区的空气质量较好?
(2)考虑用频率估计概率的方法,试根据统计数据,估计甲城区某一天空气质量等级为3
(3)分别从甲、乙两个城区的统计数据中任取一个,试求这两城区空气质量等级相同的概率.