题目内容
【题目】设函数f(x)=3ax2+2bx+c,且有a+b+c=0,f(0)>0,f(1)>0.
(Ⅰ)求证:a>0,且﹣2< ![]() <﹣1;
<﹣1;
(Ⅱ)求证:函数y=f(x)在区间(0,1)内有两个不同的零点.
【答案】证明:(Ⅰ)∵函数f(x)=3ax2+2bx+c,f(0)>0,f(1)>0,
∴c>0,3a+2b+c>0,
由条件a+b+c=0,消去b,得a>c>0;
由条件a+b+c=0,消去c,得a+b<0,2a+b>0,即﹣2a<b<﹣a,
∴ ![]()
(Ⅱ)抛物线f(x)=3ax2+2bx+c的顶点为  ,
,
由 ![]() ,得
,得 ![]() ,即有
,即有 ![]() ,
,
又∵f(0)>0,f(1)>0, ![]() ,且图象连续不断,
,且图象连续不断,
∴函数y=f(x)在区间 ![]() 与
与 ![]() 内分别有一个零点,
内分别有一个零点,
故函数y=f(x)在(0,1)内有两个不同的零点
【解析】(I)由a+b+c=0,f(0)>0,f(1)>0,消去b,得a>c>0,消去c,得a+b<0,2a+b>0,即﹣2a<b<﹣a,进而可得a>0,且﹣2< ![]() <﹣1;(Ⅱ)抛物线f(x)=3ax2+2bx+c的顶点为
<﹣1;(Ⅱ)抛物线f(x)=3ax2+2bx+c的顶点为 ![]() ,结合(1)中结论,可得
,结合(1)中结论,可得 ![]() 且f(0)>0,f(1)>0,
且f(0)>0,f(1)>0, ![]() ,且图象连续不断,由函数零点存在定理可得结论.
,且图象连续不断,由函数零点存在定理可得结论.
【考点精析】掌握二次函数的性质是解答本题的根本,需要知道当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减.
上递减.

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案【题目】某车间为了规定工时定额,需要确定加工零件所花费的时间,为此做了四次试验,得到的数据如表:
零件的个数x(个) | 2 | 3 | 4 | 5 |
加工的时间y(小时) | 2.5 | 3 | 4 | 4.5 |
(1)求出y关于x的线性回归方程 ![]() ;
;
(2)试预测加工10个零件需要多少小时?
(参考公式: ![]() =
= 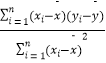 =
= 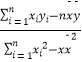 ;
; ![]() ;)
;)
【题目】甲、乙两名运动员的5次测试成绩如下图所示:
甲 | 茎 | 乙 |
5 7 | 1 | 6 8 |
8 8 2 | 2 | 3 6 7 |
设s1 , s2分别表示甲、乙两名运动员测试成绩的标准差, ![]() 分别表示甲、乙两名运动员测试成绩的平均数,则有( )
分别表示甲、乙两名运动员测试成绩的平均数,则有( )
A.![]() ,s1<s2
,s1<s2
B.![]() ,s1>s2
,s1>s2
C.![]() ,s1>s2
,s1>s2
D.![]() ,s1=s2
,s1=s2
【题目】某商场计划销售某种产品,现邀请生产该产品的甲、乙两个厂家进场试销![]() 天,两个厂家提供的返利,方案如下:甲厂家每天固定返利
天,两个厂家提供的返利,方案如下:甲厂家每天固定返利![]() 元,且每卖出一件产品厂家再返利
元,且每卖出一件产品厂家再返利![]() 元,乙厂家无固定返利,卖出
元,乙厂家无固定返利,卖出![]() 件以内(含
件以内(含![]() 件)的产品,每件产品厂家返利
件)的产品,每件产品厂家返利![]() 元,超出
元,超出![]() 件的部分每件返利
件的部分每件返利![]() 元,分别记录其
元,分别记录其![]() 天内的销售件数,得到如下频数表:
天内的销售件数,得到如下频数表:
甲厂家销售件数频数表:
销售件数 |
|
|
|
|
|
天数 |
|
|
|
|
|
乙厂家销售件数频数表:
销售件数 |
|
|
|
|
|
天数 |
|
|
|
|
|
(1) 现从甲厂家试销的![]() 天中抽取两天,求一天销售量大于
天中抽取两天,求一天销售量大于![]() 而另一天销售量小于
而另一天销售量小于![]() 的概率;
的概率;
(2)若将频率视作概率,回答以下问题:
①记乙厂家的日返利为![]() (单位:元),求
(单位:元),求![]() 的分布列和数学期望;
的分布列和数学期望;
②商场拟在甲、乙两个厂家中选择一家长期销售,如果仅从日返利额的角度考虑,请利用所学的统计学知识为商场作出选择,并说明理由.


