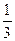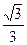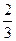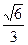题目内容
2条直线将一个平面最多分成4部分,3条直线将一个平面最多分成7部分, 4条直线将一个平面最多分成11部分,……;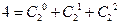 ,
,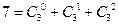 ,
,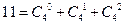 ;……
;……
(1)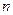 条直线将一个平面最多分成多少个部分(
条直线将一个平面最多分成多少个部分(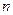 >1)?证明你的结论;
>1)?证明你的结论;
(2)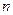 个平面最多将空间分割成多少个部分(
个平面最多将空间分割成多少个部分(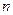 >2)?证明你的结论
>2)?证明你的结论
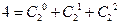 ,
,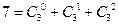 ,
,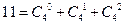 ;……
;……(1)
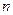 条直线将一个平面最多分成多少个部分(
条直线将一个平面最多分成多少个部分(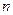 >1)?证明你的结论;
>1)?证明你的结论;(2)
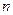 个平面最多将空间分割成多少个部分(
个平面最多将空间分割成多少个部分(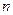 >2)?证明你的结论
>2)?证明你的结论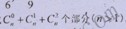
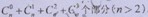
略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
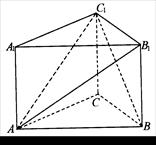
 的棱长为1,点
的棱长为1,点 是棱
是棱 的中点,点
的中点,点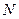 是棱
是棱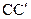 的中点,点
的中点,点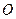 是上底面
是上底面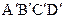 的中心.
的中心.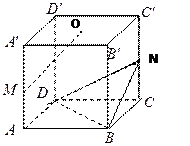 (Ⅰ)求证:MO∥平面NBD;
(Ⅰ)求证:MO∥平面NBD;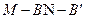 的大小;
的大小;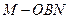 的体积.
的体积. 平面
平面 是正三角形,
是正三角形, 。
。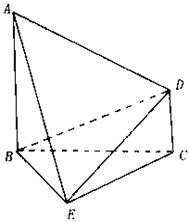
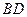 与
与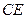 所成角的余弦值;
所成角的余弦值;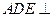 平面
平面 ;
; 的余弦值。
的余弦值。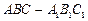 的底面正三角形的边长是2,D是
的底面正三角形的边长是2,D是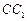 的中点,直线
的中点,直线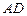 与侧面
与侧面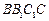 所成的角是
所成的角是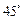 .
.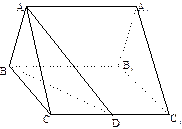
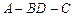 的大小;
的大小;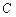 到平面
到平面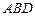 的距离.
的距离.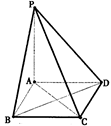
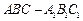 中,侧面
中,侧面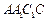
 底面
底面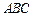 ,
,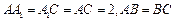 ,
, ,O为
,O为 中点.
中点.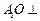 平面
平面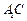 与平面
与平面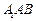 所成角的正弦值;
所成角的正弦值;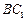 上是否存在一点
上是否存在一点 ,使得
,使得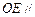 平面
平面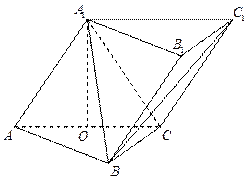
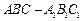 中,
中,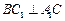 .有下列条件:
.有下列条件: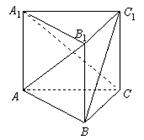
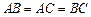 ;②
;②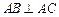 ;③
;③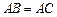 .其中能成为
.其中能成为 的充要条件的是(填上该条件的序号)________。
的充要条件的是(填上该条件的序号)________。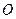 的半径为1,
的半径为1,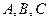 三点都在球面上,且每两点间的球面距离均为
三点都在球面上,且每两点间的球面距离均为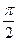 ,则球心
,则球心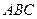 的距离为
的距离为