题目内容

1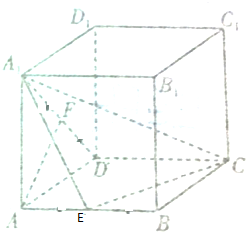．如图，在长方体ABCD-A1B1C1D1中，AD=AA1=3，AB=$\sqrt{6}$，E，F分别为AB，AD1的中点．求证：AF∥A1EC．

分析 取A1C中点P，由A1CD三角形中F和P都为中点，可证FPAE是平行四边型，从而证明AF∥EP，即可证明AF∥平面A1EC．

解答 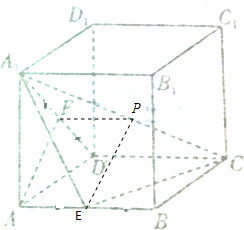证明：取A1C中点P，
因为A1CD三角形中F和P都为中点，
所以FP平行且等于CD的一半，
所以FPAE是平行四边型，
所以AF∥EP，
EP?A1EC，所以AF∥平面A1EC．

点评 本题主要考查了直线与平面平行的判定，三角形中位线的性质，考查了空间想象能力和推论论证能力，属于基本知识的考查．

练习册系列答案
相关题目
11．某次知识竞赛中有6道题，其中3道甲类题A、B、C，3道乙类题X、Y、Z，张同学从中任意抽取2道解答题．试求：
（Ⅰ）所抽取的2道题都是甲类题的概率；
（Ⅱ）所抽取的2道题不是同一类题的概率．
12．已知tanα，tanβ是方程x2+3$\sqrt{3}$x+4=0的两根，则tan（α+β）等于（　　）
A．-3B．-$\sqrt{3}$C．$\sqrt{3}$D．3
9．已知函数f（x）=cos（-$\frac{x}{2}$）+sin（$π-\frac{x}{2}$），x∈R
（1）求函数f（x）的最小正周期与最大值
（2）求函数f（x）在[0，π）上单调递减区间．
16．已知函数g（x）=acos（$\frac{π}{6}$-x），f（x）=g（x）+2cos2（x+$\frac{π}{3}$）+1（a∈R）．
（1）若x∈[-$\frac{π}{3}$，0]，求函数g（x）的最大值；
（2）若x∈[0，$\frac{5π}{6}$]，求函数f（x）的最大值．
6．已知P（B）＞0，A1A2=∅，则下列式子成立的是（　　）
①P（A1|B）＞0②P（A1∪A2|B）=P（A1|B）+P（A2|B）③P（A1$\overrightarrow{{A}_{2}}$|B）≠0④P（$\overline{{A}_{1}{A}_{2}}$|B）=1．
A．①②③④B．②C．②③D．②④
18．设f（x）是定义在R上且周期为2的函数，在区间[-1，1]上，f（x）=$\left\{\begin{array}{l}{ax+1，-1≤x＜0}\\{\frac{bx+2}{x+1}，0≤x≤1}\end{array}\right.$，其中a，b∈R，若f（$\frac{1}{2}$）=f（$\frac{3}{2}$），则3a+2b=-2．
19．已知函数f（x）=f（4x），当x∈[1，4）时，f（x）=lnx，若区间[1，16）内，函数g（x）=f（x）-ax有三个不同的零点，则实数a的取值范围是（　　）
A．（$\frac{ln2}{2}$，$\frac{1}{e}$）B．（$\frac{ln2}{8}$，$\frac{1}{4e}$）C．（$\frac{ln2}{8}$，$\frac{1}{2e}$）D．（$\frac{ln2}{8}$，$\frac{ln2}{4}$）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网