题目内容
12.已知tanα,tanβ是方程x2+3$\sqrt{3}$x+4=0的两根,则tan(α+β)等于( )| A. | -3 | B. | -$\sqrt{3}$ | C. | $\sqrt{3}$ | D. | 3 |
分析 由条件利用韦达定理求得tanα+tanβ 和tanα•tanβ 的值,再利用两角和的正切公式求得tan(α+β)的值.
解答 解:∵tanα,tanβ是方程x2+3$\sqrt{3}$x+4=0的两根,∴tanα+tanβ=-3$\sqrt{3}$,tanα•tanβ=4,
∴tan(α+β)=$\frac{tanα+tanβ}{1-tanα•tanβ}$=$\frac{-3\sqrt{3}}{1-4}$=$\sqrt{3}$,
故选:C.
点评 本题主要考查韦达定理、两角和的正切公式的应用,属于基础题.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
2.函数y=$\frac{1}{x-1}$+lnx的定义域是( )
| A. | {x|x>1} | B. | {x|0<x<1或1<x<+∞} | C. | {x|x>0} | D. | {x|x<0或x>1} |
3.某校高三年级本学期共进行了四次阶段考试,在每份数学试卷中,第Ⅰ卷共10道选择题,每小题得对的5分,答错得0分,学生甲、乙在四次考试中选择题答错的题目数如下所示:
(1)求学生甲在这四次考试中选择题答对的题目的平均数及这四次考试中第Ⅰ卷的平均得分;
(2)记以甲每次考试答错的题目数为元素构成集合A,以乙每次考试答错的题目数为元素构成集合B,在直角坐标平面上有点P(x,y),Q(-1,-2),其中x∈A,y∈B,记直线PQ的斜率为k,求满足k≥2的事件的概率.
| 甲 | 3 | 2 | 0 | 1 |
| 乙 | 4 | 3 | 2 | 0 |
(2)记以甲每次考试答错的题目数为元素构成集合A,以乙每次考试答错的题目数为元素构成集合B,在直角坐标平面上有点P(x,y),Q(-1,-2),其中x∈A,y∈B,记直线PQ的斜率为k,求满足k≥2的事件的概率.
10.已知ABCD-A1B1C1D1是边长为1的正方体,P为线段AB1上的动点,Q为底面ABCD上的动点,则PC1+PQ最小值为( )
| A. | $1+\frac{{\sqrt{2}}}{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\frac{{1+\sqrt{5}}}{2}$ |
 某公园举办花展,其中一个展区平面图如图所示,中间区域是边长为10米的正方形ABCD,两侧区域分别是以AD、BC为直径的半圆,现在中间划出一个三角形区域MPQ,其中M为AB的中点,PQ∥AB,现有甲、乙两种花展出,甲种花的价格为2百元/平方米,填满三角形区域MPQ,乙种花的价格为4百元/平方米,填满其余区域.
某公园举办花展,其中一个展区平面图如图所示,中间区域是边长为10米的正方形ABCD,两侧区域分别是以AD、BC为直径的半圆,现在中间划出一个三角形区域MPQ,其中M为AB的中点,PQ∥AB,现有甲、乙两种花展出,甲种花的价格为2百元/平方米,填满三角形区域MPQ,乙种花的价格为4百元/平方米,填满其余区域.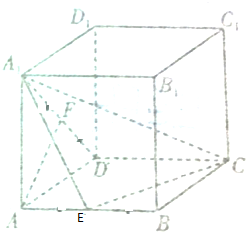 如图,在长方体ABCD-A1B1C1D1中,AD=AA1=3,AB=$\sqrt{6}$,E,F分别为AB,AD1的中点.求证:AF∥A1EC.
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=3,AB=$\sqrt{6}$,E,F分别为AB,AD1的中点.求证:AF∥A1EC.