题目内容
18.设f(x)是定义在R上且周期为2的函数,在区间[-1,1]上,f(x)=$\left\{\begin{array}{l}{ax+1,-1≤x<0}\\{\frac{bx+2}{x+1},0≤x≤1}\end{array}\right.$,其中a,b∈R,若f($\frac{1}{2}$)=f($\frac{3}{2}$),则3a+2b=-2.分析 根据函数的周期性将以f($\frac{3}{2}$)转为f(-$\frac{1}{2}$),根据已知的函数的解析式化简已知的方程,即可求出3a+2b的值.
解答 解:因为f(x)是定义在R上且周期为2的函数,
所以f($\frac{3}{2}$)=f($\frac{3}{2}$-2)=f(-$\frac{1}{2}$),
因为f($\frac{1}{2}$)=f($\frac{3}{2}$),所以f($\frac{1}{2}$)=f(-$\frac{1}{2}$),
因为在区间[-1,1]上,f(x)=$\left\{\begin{array}{l}{ax+1,-1≤x<0}\\{\frac{bx+2}{x+1},0≤x≤1}\end{array}\right.$,
所以$\frac{b×\frac{1}{2}+2}{\frac{1}{2}+1}=a(-\frac{1}{2})+1$,化简得3a+2b=-2,
故答案为:-2.
点评 本题考查了函数周期性的应用,以及分段函数求值,属于基础题.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
6.点P在正方体ABCD-A1B1C1D1的面对角线BC1上运动,则下列四个命题:
①三棱锥A1-D1DP的体积不变;
②A1P∥平面ACD1;
③DP⊥BC1;
④平面A1PB⊥平面PDB1.
其中正确的命题的序号是( )
①三棱锥A1-D1DP的体积不变;
②A1P∥平面ACD1;
③DP⊥BC1;
④平面A1PB⊥平面PDB1.
其中正确的命题的序号是( )
| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
3.方程lgx-4+x=0的根一定位于区间( )
| A. | (5,6) | B. | (3,4) | C. | (2,3) | D. | (1,2) |
10.已知ABCD-A1B1C1D1是边长为1的正方体,P为线段AB1上的动点,Q为底面ABCD上的动点,则PC1+PQ最小值为( )
| A. | $1+\frac{{\sqrt{2}}}{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\frac{{1+\sqrt{5}}}{2}$ |
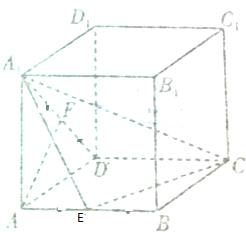 如图,在长方体ABCD-A1B1C1D1中,AD=AA1=3,AB=$\sqrt{6}$,E,F分别为AB,AD1的中点.求证:AF∥A1EC.
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=3,AB=$\sqrt{6}$,E,F分别为AB,AD1的中点.求证:AF∥A1EC. 如图,在四棱台ABCD-A1B1C1D1中,DD1⊥底面ABCD,四边形ABCD为正方形,DD1=AD=2,A1B1=1,C1E∥平面 ADD1A1.
如图,在四棱台ABCD-A1B1C1D1中,DD1⊥底面ABCD,四边形ABCD为正方形,DD1=AD=2,A1B1=1,C1E∥平面 ADD1A1.