题目内容
6.已知P(B)>0,A1A2=∅,则下列式子成立的是( )①P(A1|B)>0②P(A1∪A2|B)=P(A1|B)+P(A2|B)③P(A1$\overrightarrow{{A}_{2}}$|B)≠0④P($\overline{{A}_{1}{A}_{2}}$|B)=1.
| A. | ①②③④ | B. | ② | C. | ②③ | D. | ②④ |
分析 先根据条件得到事件A1与A2互斥,再根据条件概率的性质即可判断.
解答 解:∵P(B)>0,A1A2=∅,
∴事件A1与A2互斥,
由条件概率的性质可知,①P(A1|B)≥0②P(A1∪A2|B)=P(A1|B)+P(A2|B)③P(A1$\overrightarrow{{A}_{2}}$|B)≥0④P($\overline{{A}_{1}{A}_{2}}$|B)≥0,
故②正确,其它错误,
故选:B.
点评 本题考查了条件概率的性质和互斥事件,属于基础题.

练习册系列答案
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
16.阅读如图所示的程序框图,输出S的值是( )


| A. | 0 | B. | $\sqrt{3}$ | C. | -$\sqrt{3}$ | D. | -$\frac{\sqrt{3}}{2}$ |
6.点P在正方体ABCD-A1B1C1D1的面对角线BC1上运动,则下列四个命题:
①三棱锥A1-D1DP的体积不变;
②A1P∥平面ACD1;
③DP⊥BC1;
④平面A1PB⊥平面PDB1.
其中正确的命题的序号是( )
①三棱锥A1-D1DP的体积不变;
②A1P∥平面ACD1;
③DP⊥BC1;
④平面A1PB⊥平面PDB1.
其中正确的命题的序号是( )
| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
3.方程lgx-4+x=0的根一定位于区间( )
| A. | (5,6) | B. | (3,4) | C. | (2,3) | D. | (1,2) |
4. 如图,在Rt△ABC中,AB=4,AC=3,∠CAB=90°,以点B为一个焦点作一个椭圆,使这个椭圆的另一个焦点在AC边上,且这个椭圆过A、C两点,则椭圆的离心率为( )
如图,在Rt△ABC中,AB=4,AC=3,∠CAB=90°,以点B为一个焦点作一个椭圆,使这个椭圆的另一个焦点在AC边上,且这个椭圆过A、C两点,则椭圆的离心率为( )
 如图,在Rt△ABC中,AB=4,AC=3,∠CAB=90°,以点B为一个焦点作一个椭圆,使这个椭圆的另一个焦点在AC边上,且这个椭圆过A、C两点,则椭圆的离心率为( )
如图,在Rt△ABC中,AB=4,AC=3,∠CAB=90°,以点B为一个焦点作一个椭圆,使这个椭圆的另一个焦点在AC边上,且这个椭圆过A、C两点,则椭圆的离心率为( )| A. | $\frac{\sqrt{5}}{3}$ | B. | $\frac{2\sqrt{5}}{3}$ | C. | $\frac{2\sqrt{5}}{5}$ | D. | $\frac{1}{2}$ |
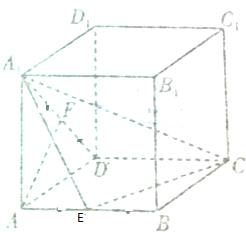 如图,在长方体ABCD-A1B1C1D1中,AD=AA1=3,AB=$\sqrt{6}$,E,F分别为AB,AD1的中点.求证:AF∥A1EC.
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=3,AB=$\sqrt{6}$,E,F分别为AB,AD1的中点.求证:AF∥A1EC.