题目内容
16.已知函数g(x)=acos($\frac{π}{6}$-x),f(x)=g(x)+2cos2(x+$\frac{π}{3}$)+1(a∈R).(1)若x∈[-$\frac{π}{3}$,0],求函数g(x)的最大值;
(2)若x∈[0,$\frac{5π}{6}$],求函数f(x)的最大值.
分析 (1)直接利用三角函数的最值求解就.
(2)通过同角三角函数的基本关系式化简表达式,然后利用二次函数闭区间是的最值求解最值.注意a的讨论.
解答 解:(1)∵x∈[-$\frac{π}{3}$,0],
∴$\frac{π}{6}$-x∈[$\frac{π}{6}$,$\frac{π}{2}$]
∴cos($\frac{π}{6}$-x)∈[0,$\frac{\sqrt{3}}{2}$],
∴当a>0时,函数g(x)的最大值为:$\frac{\sqrt{3}a}{2}$.
当a≤0时,函数g(x)的最大值为:0.
(2)∵x∈[0,$\frac{5π}{6}$],
∴f(x)=g(x)+2cos2(x+$\frac{π}{3}$)+1
=acos($\frac{π}{6}$-x)+2cos2(x+$\frac{π}{3}$)+1
=acos($\frac{π}{6}$-x)+2sin2($\frac{π}{2}$-x$-\frac{π}{3}$)+1
=acos($\frac{π}{6}$-x)-2cos2($\frac{π}{6}$-x)+3,
令t=cos($\frac{π}{6}$-x),
可得f(x)=at-2t2+3=-2(t-$\frac{a}{4}$)2+$\frac{{a}^{2}}{8}$+3,t∈[0,$\frac{\sqrt{3}}{2}$],
当$\frac{a}{4}$>$\frac{\sqrt{3}}{2}$,即a>2$\sqrt{3}$时,t=$\frac{\sqrt{3}}{2}$时,最大值为:$\frac{3+\sqrt{3}a}{2}$.
当$\frac{a}{4}$∈[0,$\frac{\sqrt{3}}{2}$],即0≤a≤2$\sqrt{3}$,t=$\frac{a}{4}$时,最大值为:$\frac{{a}^{2}}{8}$+3.
当$\frac{a}{4}$<0时,即a<0,t=0时,最大值为:3.
点评 本题考查三角函数的最值的求法,换元法以及二次函数闭区间上的最值的求法,考查分类讨论转化是的应用.

 名校课堂系列答案
名校课堂系列答案| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | |x1-(a+bx1)|+|x2-(a+bx2)|+|x3-(a+bx3)| | B. | [x1-(a+bx1)]2+[x2-(a+bx2)]2+[x3-(a+bx3)]2 | ||
| C. | |y1-(a+bx1)|+|y2-(a+bx2)|+|y3-(a+bx3)| | D. | [y1-(a+bx1)]2+[y2-(a+bx2)]2+[y3-(a+bx3)]2 |
| 分组 | 频数 | 频率 | 频率/组距 |
| (40,50] | 2 | 0.02 | 0.002 |
| (50,60] | 4 | 0.04 | 0.004 |
| (60,70] | 11 | 0.11 | 0.011 |
| (70,80] | 38 | 0.38 | 0.038 |
| (80,90] | m | n | p |
| (90,100] | 11 | 0.11 | 0.011 |
| 合计 | M | N | P |
(2)为了了解某些同学在数学学习中存在的问题,现从样本中分数在(40,60]中的6位同学中任意抽取2人进行调查,求分数在(40,50]和(50,60]中各有一人的概率.
 某公园举办花展,其中一个展区平面图如图所示,中间区域是边长为10米的正方形ABCD,两侧区域分别是以AD、BC为直径的半圆,现在中间划出一个三角形区域MPQ,其中M为AB的中点,PQ∥AB,现有甲、乙两种花展出,甲种花的价格为2百元/平方米,填满三角形区域MPQ,乙种花的价格为4百元/平方米,填满其余区域.
某公园举办花展,其中一个展区平面图如图所示,中间区域是边长为10米的正方形ABCD,两侧区域分别是以AD、BC为直径的半圆,现在中间划出一个三角形区域MPQ,其中M为AB的中点,PQ∥AB,现有甲、乙两种花展出,甲种花的价格为2百元/平方米,填满三角形区域MPQ,乙种花的价格为4百元/平方米,填满其余区域.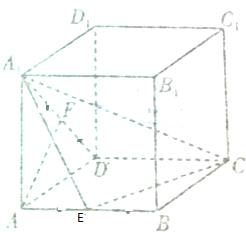 如图,在长方体ABCD-A1B1C1D1中,AD=AA1=3,AB=$\sqrt{6}$,E,F分别为AB,AD1的中点.求证:AF∥A1EC.
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=3,AB=$\sqrt{6}$,E,F分别为AB,AD1的中点.求证:AF∥A1EC.