题目内容
11.某次知识竞赛中有6道题,其中3道甲类题A、B、C,3道乙类题X、Y、Z,张同学从中任意抽取2道解答题.试求:(Ⅰ)所抽取的2道题都是甲类题的概率;
(Ⅱ)所抽取的2道题不是同一类题的概率.
分析 根据排列组合求出所抽取的2道题的基本事件共有15种,
(1)所抽取的2道题都是甲类题有3种,利用古典概型计算即可;
(2)所抽取的2道题不是同一类题的有9种,利用古典概型计算即可.
解答 解:知识竞赛中有6道题,其中3道甲类题A、B、C,3道乙类题X、Y、Z,张同学从中任意抽取2道解答题,共有${C}_{6}^{2}$=15种,
(1)所抽取的2道题都是甲类题有${C}_{3}^{2}$=3种,
故所抽取的2道题都是甲类题的概率P=$\frac{3}{15}$=$\frac{1}{5}$,;
(Ⅱ),所抽取的2道题不是同一类题的有${C}_{3}^{1}•{C}_{3}^{1}$=9种,
故所抽取的2道题不是同一类题的概率P=$\frac{9}{15}$=$\frac{3}{5}$.
点评 本题考查组合的运用以及古典概型的概率的计算,属于基础题

练习册系列答案
相关题目
1.命题p:y=|sinx|是偶函数,命题q:y=sin|x|是周期为π的周期函数,则下列命题中为真命题的是( )
| A. | p∧q | B. | p∨q | C. | (¬p)∧q | D. | (¬p)∨q |
2.函数y=$\frac{1}{x-1}$+lnx的定义域是( )
| A. | {x|x>1} | B. | {x|0<x<1或1<x<+∞} | C. | {x|x>0} | D. | {x|x<0或x>1} |
19.以(1,2)为圆心,$\sqrt{5}$为半径的圆的方程为( )
| A. | x2+y2-2x+4y=0 | B. | x2+y2+2x+4y=0 | C. | x2+y2-2x-4y=0 | D. | x2+y2+2x-4y=0 |
6.“-1<k<1”是“方程$\frac{{x}^{2}}{k-1}$+$\frac{{y}^{2}}{k+1}$=1表示双曲线”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
16.阅读如图所示的程序框图,输出S的值是( )
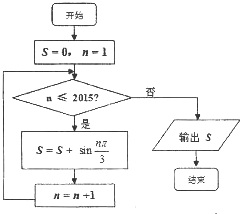

| A. | 0 | B. | $\sqrt{3}$ | C. | -$\sqrt{3}$ | D. | -$\frac{\sqrt{3}}{2}$ |
3.某校高三年级本学期共进行了四次阶段考试,在每份数学试卷中,第Ⅰ卷共10道选择题,每小题得对的5分,答错得0分,学生甲、乙在四次考试中选择题答错的题目数如下所示:
(1)求学生甲在这四次考试中选择题答对的题目的平均数及这四次考试中第Ⅰ卷的平均得分;
(2)记以甲每次考试答错的题目数为元素构成集合A,以乙每次考试答错的题目数为元素构成集合B,在直角坐标平面上有点P(x,y),Q(-1,-2),其中x∈A,y∈B,记直线PQ的斜率为k,求满足k≥2的事件的概率.
| 甲 | 3 | 2 | 0 | 1 |
| 乙 | 4 | 3 | 2 | 0 |
(2)记以甲每次考试答错的题目数为元素构成集合A,以乙每次考试答错的题目数为元素构成集合B,在直角坐标平面上有点P(x,y),Q(-1,-2),其中x∈A,y∈B,记直线PQ的斜率为k,求满足k≥2的事件的概率.
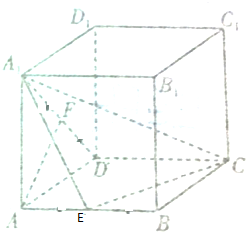 如图,在长方体ABCD-A1B1C1D1中,AD=AA1=3,AB=$\sqrt{6}$,E,F分别为AB,AD1的中点.求证:AF∥A1EC.
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=3,AB=$\sqrt{6}$,E,F分别为AB,AD1的中点.求证:AF∥A1EC.