题目内容
19.已知函数f(x)=f(4x),当x∈[1,4)时,f(x)=lnx,若区间[1,16)内,函数g(x)=f(x)-ax有三个不同的零点,则实数a的取值范围是( )| A. | ($\frac{ln2}{2}$,$\frac{1}{e}$) | B. | ($\frac{ln2}{8}$,$\frac{1}{4e}$) | C. | ($\frac{ln2}{8}$,$\frac{1}{2e}$) | D. | ($\frac{ln2}{8}$,$\frac{ln2}{4}$) |
分析 化简f(x)=$\left\{\begin{array}{l}{lnx,1≤x<4}\\{ln\frac{x}{4},4≤x<16}\end{array}\right.$,作函数的图象,结合函数图象可得.
解答 解:∵f(x)=f(4x),且当x∈[1,4)时,f(x)=lnx;
∴f(x)=$\left\{\begin{array}{l}{lnx,1≤x<4}\\{ln\frac{x}{4},4≤x<16}\end{array}\right.$;
作函数f(x)=$\left\{\begin{array}{l}{lnx,1≤x<4}\\{ln\frac{x}{4},4≤x<16}\end{array}\right.$与函数y=ax的图象如下,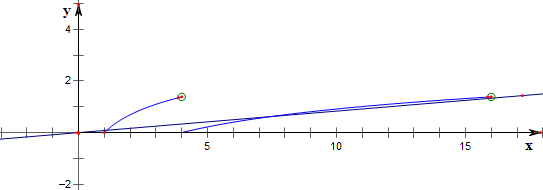
结合图象可知,
当直线y=ax与f(x)=ln$\frac{x}{4}$相切时,
即$\frac{ln\frac{x}{4}}{x}$=$\frac{1}{x}$,
从而可得x=4e;
a=$\frac{1}{4e}$;
当过点(16,ln4)时,
a=$\frac{ln4}{16}$=$\frac{ln2}{8}$;
结合图象可得,
$\frac{ln2}{8}$<a<$\frac{1}{4e}$;
故选B.
点评 本题考查了导数的综合应用及数形结合的思想应用,属于中档题.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
10.已知ABCD-A1B1C1D1是边长为1的正方体,P为线段AB1上的动点,Q为底面ABCD上的动点,则PC1+PQ最小值为( )
| A. | $1+\frac{{\sqrt{2}}}{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\frac{{1+\sqrt{5}}}{2}$ |
14.某校高二年级的一次数学考试中,为了分析学生的得分情况,随机抽取M名同学的成绩,数据的分组统计表如下:
(1)求出表中M,n的值;
(2)为了了解某些同学在数学学习中存在的问题,现从样本中分数在(40,60]中的6位同学中任意抽取2人进行调查,求分数在(40,50]和(50,60]中各有一人的概率.
| 分组 | 频数 | 频率 | 频率/组距 |
| (40,50] | 2 | 0.02 | 0.002 |
| (50,60] | 4 | 0.04 | 0.004 |
| (60,70] | 11 | 0.11 | 0.011 |
| (70,80] | 38 | 0.38 | 0.038 |
| (80,90] | m | n | p |
| (90,100] | 11 | 0.11 | 0.011 |
| 合计 | M | N | P |
(2)为了了解某些同学在数学学习中存在的问题,现从样本中分数在(40,60]中的6位同学中任意抽取2人进行调查,求分数在(40,50]和(50,60]中各有一人的概率.
4.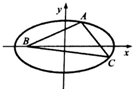 如图,在Rt△ABC中,AB=4,AC=3,∠CAB=90°,以点B为一个焦点作一个椭圆,使这个椭圆的另一个焦点在AC边上,且这个椭圆过A、C两点,则椭圆的离心率为( )
如图,在Rt△ABC中,AB=4,AC=3,∠CAB=90°,以点B为一个焦点作一个椭圆,使这个椭圆的另一个焦点在AC边上,且这个椭圆过A、C两点,则椭圆的离心率为( )
 如图,在Rt△ABC中,AB=4,AC=3,∠CAB=90°,以点B为一个焦点作一个椭圆,使这个椭圆的另一个焦点在AC边上,且这个椭圆过A、C两点,则椭圆的离心率为( )
如图,在Rt△ABC中,AB=4,AC=3,∠CAB=90°,以点B为一个焦点作一个椭圆,使这个椭圆的另一个焦点在AC边上,且这个椭圆过A、C两点,则椭圆的离心率为( )| A. | $\frac{\sqrt{5}}{3}$ | B. | $\frac{2\sqrt{5}}{3}$ | C. | $\frac{2\sqrt{5}}{5}$ | D. | $\frac{1}{2}$ |
11.若曲线y=ex-$\frac{a}{e^x}$(a>0)上任意一点切线的倾斜角的取值范围是[${\frac{π}{3}$,$\frac{π}{2}}$),则a=( )
| A. | $\frac{1}{12}$ | B. | $\frac{1}{3}$ | C. | $\frac{3}{4}$ | D. | 3 |
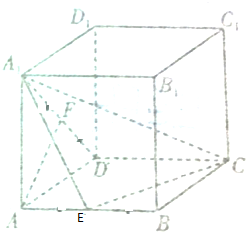 如图,在长方体ABCD-A1B1C1D1中,AD=AA1=3,AB=$\sqrt{6}$,E,F分别为AB,AD1的中点.求证:AF∥A1EC.
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=3,AB=$\sqrt{6}$,E,F分别为AB,AD1的中点.求证:AF∥A1EC.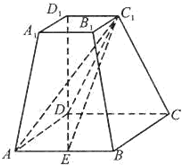 如图,在四棱台ABCD-A1B1C1D1中,DD1⊥底面ABCD,四边形ABCD为正方形,DD1=AD=2,A1B1=1,C1E∥平面 ADD1A1.
如图,在四棱台ABCD-A1B1C1D1中,DD1⊥底面ABCD,四边形ABCD为正方形,DD1=AD=2,A1B1=1,C1E∥平面 ADD1A1.