题目内容
5.椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的焦距为2$\sqrt{3}$,左、右焦点分别为F1、F2,点P是椭圆上一点,∠F1PF2=60°,△PF1F2的面积为2$\sqrt{3}$,则椭圆的标准方程为$\frac{x^2}{9}+\frac{y^2}{6}=1$.分析 由题意可得a2-b2=c2=3,|PF1|•|PF2|=8.再根据椭圆的定义可得|PF1|+|PF2|=2a,再利用余弦定理求得a2 的值,可得b2 的值,从而得到要求的椭圆的方程.
解答 解:由题意可得c=$\sqrt{3}$,∴a2-b2=c2=3.
由∠F1PF2=60°,△PF1F2的面积为2$\sqrt{3}$,可得$\frac{1}{2}$|PF1|•|PF2|•sin∠F1PF2=$\frac{\sqrt{3}}{4}$|PF1|•|PF2|=2$\sqrt{3}$,
∴|PF1|•|PF2|=8.
再根据椭圆的定义可得|PF1|+|PF2|=2a.
再利用余弦定理可得4c2=12=${{PF}_{1}}^{2}$+${{PF}_{2}}^{2}$-2PF1•PF2•cos60°=${{(PF}_{1}{+PF}_{2})}^{2}$-3PF1•PF2=4a2-3×8,
求得a2=9,∴b2=6,
故要求的椭圆的方程为 $\frac{x^2}{9}+\frac{y^2}{6}=1$,
故答案为:$\frac{x^2}{9}+\frac{y^2}{6}=1$.
点评 本题主要考查余弦定理,椭圆的定义、标准方程,以及简单性质的应用,属于基础题.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案
相关题目
20.执行如图的程序框图,若输出的n=5,则输入整数p的最大值是( )
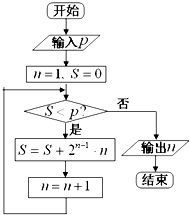

| A. | 47 | B. | 48 | C. | 49 | D. | 50 |
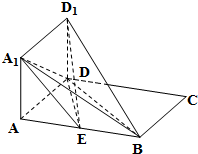 如图所示,正方形AA1D1D与矩形ABCD所在平面互相垂直,AB=2AD=2,点E为AB的中点.求直线D1E与平面A1D1B所成角的正弦值.
如图所示,正方形AA1D1D与矩形ABCD所在平面互相垂直,AB=2AD=2,点E为AB的中点.求直线D1E与平面A1D1B所成角的正弦值.