题目内容
17.定义在R上的函数f(x)满足f(x+2)=f(x)+1,且x∈[0,1]时,f(x)=4x,x∈(1,2)时,f(x)=$\frac{f(1)}{x}$,令g(x)=2f(x)-x-4,x∈[-6,2],则函数g(x)的零点个数为( )| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
分析 由x∈[0,1]时,f(x)=4x,可得f(1)=4,x∈(1,2)时,f(x)=$\frac{f(1)}{x}$=$\frac{4}{x}$,而由函数f(x)满足f(x+2)=f(x)+1,即自变量x每增加2个单位,函数图象向上平移1个单位,自变量每减少2个单位,函数图象向下平移1个单位,画出函数图象,结合函数的图象可求
解答 解:∵x∈[0,1]时,f(x)=4x,
∴f(1)=4
∴x∈(1,2)时,f(x)=$\frac{f(1)}{x}$=$\frac{4}{x}$,
∵g(x)=2f(x)-x-4,x∈[-6,2],
令g(x)=2f(x)-x-4=0,
即f(x)=$\frac{1}{2}$x+2
∵函数f(x)满足f(x+2)=f(x)+1,即自变量x每增加2个单位,函数图象向上平移1个单位,自变量每减少2个单位,函数图象向下平移1个单位,
分别画出函数y=f(x)在x∈[-6,2],y=$\frac{1}{2}$x+2的图象,
∴y=f(x)在x∈[-6,2],y=$\frac{1}{2}$x+2有8个交点,
故函数g(x)的零点个数为8个.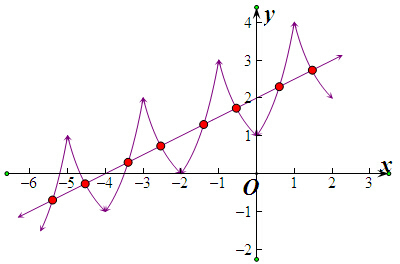
故选:C
点评 本题考查的知识点是对数函数的图象与性质,利用转化思想,将函数的零点个数问题,转化为函数图象交点个数问题,是解答本题的关键

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
12.设a=log3$\sqrt{3}$,b=ln2,c=5${\;}^{-\frac{1}{2}}$,则( )
| A. | c>b>a | B. | b>a>c | C. | a>c>b | D. | a>b>c |
 如图,在平面四边形ABCD中,AD=1,CD=2,AC=$\sqrt{7}$,则cos∠CAD=$\frac{2\sqrt{7}}{7}$;又若cos∠BAD=-$\frac{\sqrt{7}}{14}$,sin∠CBA=$\frac{\sqrt{21}}{6}$,则BC=3.
如图,在平面四边形ABCD中,AD=1,CD=2,AC=$\sqrt{7}$,则cos∠CAD=$\frac{2\sqrt{7}}{7}$;又若cos∠BAD=-$\frac{\sqrt{7}}{14}$,sin∠CBA=$\frac{\sqrt{21}}{6}$,则BC=3. 如图:四棱锥P-ABCD中,底面ABCD是边长为2的正方形,平面PCD⊥底面ABCD,且PC=PD=a.
如图:四棱锥P-ABCD中,底面ABCD是边长为2的正方形,平面PCD⊥底面ABCD,且PC=PD=a.