题目内容
12.曲线y=lnx在点A(e,1)处的切线斜率为 ( )| A. | 1 | B. | 2 | C. | $\frac{1}{e}$ | D. | e |
分析 求出曲线的导函数,把切点的横坐标e代入即可求出切线的斜率.
解答 解:求导数可定y′=$\frac{1}{x}$,切点为M(e,1),
则切线的斜率k=$\frac{1}{e}$,
故选:C.
点评 本题考查导数的几何意义,考查学生会根据导函数求切线的斜率,比较基础.

练习册系列答案
相关题目
3.方程lgx-4+x=0的根一定位于区间( )
| A. | (5,6) | B. | (3,4) | C. | (2,3) | D. | (1,2) |
4. 如图,在Rt△ABC中,AB=4,AC=3,∠CAB=90°,以点B为一个焦点作一个椭圆,使这个椭圆的另一个焦点在AC边上,且这个椭圆过A、C两点,则椭圆的离心率为( )
如图,在Rt△ABC中,AB=4,AC=3,∠CAB=90°,以点B为一个焦点作一个椭圆,使这个椭圆的另一个焦点在AC边上,且这个椭圆过A、C两点,则椭圆的离心率为( )
 如图,在Rt△ABC中,AB=4,AC=3,∠CAB=90°,以点B为一个焦点作一个椭圆,使这个椭圆的另一个焦点在AC边上,且这个椭圆过A、C两点,则椭圆的离心率为( )
如图,在Rt△ABC中,AB=4,AC=3,∠CAB=90°,以点B为一个焦点作一个椭圆,使这个椭圆的另一个焦点在AC边上,且这个椭圆过A、C两点,则椭圆的离心率为( )| A. | $\frac{\sqrt{5}}{3}$ | B. | $\frac{2\sqrt{5}}{3}$ | C. | $\frac{2\sqrt{5}}{5}$ | D. | $\frac{1}{2}$ |
1.已知x、y满足约束条件$\left\{\begin{array}{l}x≤a\\ x-2y+3≤0\\ 2x-y+3≥0\end{array}\right.$,且z=x+2y的最大值为11,则a=( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
2.y=2sinx-cosx的最大值为( )
| A. | 1 | B. | 3 | C. | $\sqrt{5}$ | D. | $\sqrt{3}$ |
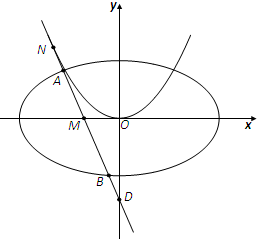 椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,且以原点为圆心,椭圆的短半轴长为半径的圆与直线x-y+$\sqrt{2}$=0相切.
椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,且以原点为圆心,椭圆的短半轴长为半径的圆与直线x-y+$\sqrt{2}$=0相切.