题目内容
2.y=2sinx-cosx的最大值为( )| A. | 1 | B. | 3 | C. | $\sqrt{5}$ | D. | $\sqrt{3}$ |
分析 由辅助角公式可得y=$\sqrt{5}$sin(x-φ),其中tanφ=$\frac{1}{2}$,易得函数的最大值.
解答 解:化简可得y=2sinx-cosx
=$\sqrt{5}$($\frac{2}{\sqrt{5}}$sinx-$\frac{1}{\sqrt{5}}$cosx)
=$\sqrt{5}$sin(x-φ),其中tanφ=$\frac{1}{2}$,
∴函数的最大值为$\sqrt{5}$
故选:C.
点评 本题考查三角函数的最值,涉及辅助角公式,属基础题.

练习册系列答案
相关题目
12.曲线y=lnx在点A(e,1)处的切线斜率为 ( )
| A. | 1 | B. | 2 | C. | $\frac{1}{e}$ | D. | e |
14.已知f(x)=$\left\{\begin{array}{l}{x+2(x≤-1)}\\{{x}^{2}(x>-1)}\end{array}\right.$,若f(x)=3,则x的值是( )
| A. | 1 | B. | 1或±$\sqrt{3}$ | C. | ±$\sqrt{3}$ | D. | $\sqrt{3}$ |
11.直线y=kx+b通过第一、三、四象限,则有( )
| A. | d>0,b>0 | B. | k>0,b<0 | C. | k<0,b>0 | D. | k<0,b<0 |
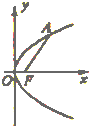 如图,F是抛物线E:y2=2px(p>0)的焦点,A是抛物线E上任意一点.现给出下列四个结论:
如图,F是抛物线E:y2=2px(p>0)的焦点,A是抛物线E上任意一点.现给出下列四个结论: