题目内容
4.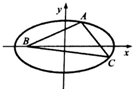 如图,在Rt△ABC中,AB=4,AC=3,∠CAB=90°,以点B为一个焦点作一个椭圆,使这个椭圆的另一个焦点在AC边上,且这个椭圆过A、C两点,则椭圆的离心率为( )
如图,在Rt△ABC中,AB=4,AC=3,∠CAB=90°,以点B为一个焦点作一个椭圆,使这个椭圆的另一个焦点在AC边上,且这个椭圆过A、C两点,则椭圆的离心率为( )| A. | $\frac{\sqrt{5}}{3}$ | B. | $\frac{2\sqrt{5}}{3}$ | C. | $\frac{2\sqrt{5}}{5}$ | D. | $\frac{1}{2}$ |
分析 通过记另一个焦点为D,易得△ABD也是直角三角形,利用勾股定理及椭圆定义可得a=3、c=$\sqrt{5}$,进而可得结论.
解答 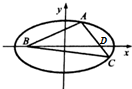 解:如图,记另一个焦点为D,则△ABD也是直角三角形.
解:如图,记另一个焦点为D,则△ABD也是直角三角形.
∵AB=4,AC=3,∠CAB=90°,
∴BC=$\sqrt{A{B}^{2}+A{C}^{2}}$=$\sqrt{{4}^{2}+{3}^{2}}$=5,
由椭圆定义可知:AB+AD=CB+CD=$\frac{1}{2}$(AB+BC+CA)=$\frac{1}{2}(3+4+5)$=6,
∴椭圆的长轴长2a=6,∴a=3,
设椭圆的焦距为2c,即BD=2c,
由椭圆定义可知:AD=2a-AB=6-4=2,
又∵AD=$\sqrt{B{D}^{2}-A{B}^{2}}$=$\sqrt{(2c)^{2}-{4}^{2}}$,
∴2=$\sqrt{(2c)^{2}-{4}^{2}}$,解得c=$\sqrt{5}$,
∴离心率e=$\frac{c}{a}$=$\frac{\sqrt{5}}{3}$,
故选:A.
点评 本题考查求椭圆的离心率,注意解题方法的积累,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.已知P(B)>0,A1A2=∅,则下列式子成立的是( )
①P(A1|B)>0②P(A1∪A2|B)=P(A1|B)+P(A2|B)③P(A1$\overrightarrow{{A}_{2}}$|B)≠0④P($\overline{{A}_{1}{A}_{2}}$|B)=1.
①P(A1|B)>0②P(A1∪A2|B)=P(A1|B)+P(A2|B)③P(A1$\overrightarrow{{A}_{2}}$|B)≠0④P($\overline{{A}_{1}{A}_{2}}$|B)=1.
| A. | ①②③④ | B. | ② | C. | ②③ | D. | ②④ |
12.曲线y=lnx在点A(e,1)处的切线斜率为 ( )
| A. | 1 | B. | 2 | C. | $\frac{1}{e}$ | D. | e |
19.已知函数f(x)=f(4x),当x∈[1,4)时,f(x)=lnx,若区间[1,16)内,函数g(x)=f(x)-ax有三个不同的零点,则实数a的取值范围是( )
| A. | ($\frac{ln2}{2}$,$\frac{1}{e}$) | B. | ($\frac{ln2}{8}$,$\frac{1}{4e}$) | C. | ($\frac{ln2}{8}$,$\frac{1}{2e}$) | D. | ($\frac{ln2}{8}$,$\frac{ln2}{4}$) |
9.设 P是双曲线C:$\frac{x^2}{4}$-y2=1上的任意一点,点 P到双曲线C的两条渐近线的距离分别为d1、d2,则d1•d2=( )
| A. | $\frac{2}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{{2\sqrt{5}}}{5}$ | D. | $\frac{{4\sqrt{5}}}{5}$ |
14.已知f(x)=$\left\{\begin{array}{l}{x+2(x≤-1)}\\{{x}^{2}(x>-1)}\end{array}\right.$,若f(x)=3,则x的值是( )
| A. | 1 | B. | 1或±$\sqrt{3}$ | C. | ±$\sqrt{3}$ | D. | $\sqrt{3}$ |
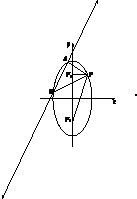 已知F1,F2是椭圆$\frac{y^2}{4}+\frac{x^2}{2}$=1的两焦点,P是椭圆在第一象限弧上一点,且满足$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}$=1,直线l:y=$\sqrt{2}$x+m与椭圆交于A,B两点.
已知F1,F2是椭圆$\frac{y^2}{4}+\frac{x^2}{2}$=1的两焦点,P是椭圆在第一象限弧上一点,且满足$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}$=1,直线l:y=$\sqrt{2}$x+m与椭圆交于A,B两点.
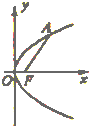 如图,F是抛物线E:y2=2px(p>0)的焦点,A是抛物线E上任意一点.现给出下列四个结论:
如图,F是抛物线E:y2=2px(p>0)的焦点,A是抛物线E上任意一点.现给出下列四个结论: