题目内容
20. 椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,且以原点为圆心,椭圆的短半轴长为半径的圆与直线x-y+$\sqrt{2}$=0相切.
椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,且以原点为圆心,椭圆的短半轴长为半径的圆与直线x-y+$\sqrt{2}$=0相切.(1)求椭圆E的方程;
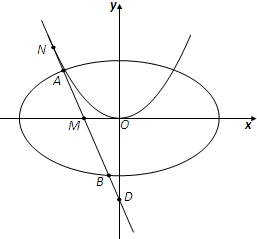
(2)已知直线l过点M(-$\frac{1}{2}$,0)且与开口向上,顶点在原点的抛物线C切于第二象限的一点N,直线l与椭圆E交于A、B两点,与y轴交于D点,若$\overrightarrow{AD}$=λ$\overrightarrow{AN}$,$\overrightarrow{BD}$=μ$\overrightarrow{BN}$,且λ+μ=-4,求抛物线C的标准方程.
分析 (1)利用离心率计算公式、以原点为圆心,椭圆的短半轴长为半径的圆与直线x-y+$\sqrt{2}$=0相切,求出a,b,即可求椭圆E的方程;
(2)设抛物线C的方程为y=ax2(a>0),直线与抛物线C切点为N(x0,ax02).利用导数的几何意义可得切线的斜率,进而得到切线方程,即可得到切点N,进一步简化切线方程,把直线l的方程与椭圆的方程联立得到根与系数的关系,再利用已知向量关系式$\overrightarrow{AD}$=λ$\overrightarrow{AN}$,$\overrightarrow{BD}$=μ$\overrightarrow{BN}$,且λ+μ=-4,即可得到a及抛物线C的标准方程.
解答 解:(1)由题意知e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$,$\frac{{a}^{2}-{b}^{2}}{{a}^{2}}=\frac{1}{2}$,
即a=$\sqrt{2}$b…(1分)
又以原点为圆心,椭圆的短半轴长为半径的圆与直线x-y+$\sqrt{2}$=0相切,
∴b=$\frac{\sqrt{2}}{\sqrt{1+1}}$=1,…(2分)
∴a=$\sqrt{2}$,
故椭圆的方程为$\frac{{x}^{2}}{2}+{y}^{2}=1$…(4分)
(2)设抛物线C的方程为y=ax2(a>0),直线l与抛物线的切点为N(x0,ax02)
∵y′=2ax,∴切线l的斜率为2ax0,
∴切线方程为y-ax02=2ax0(x-x0),
∵直线l过点M(-$\frac{1}{2}$,0),
∴-ax02=2ax0(-$\frac{1}{2}$-x0),
∵点N在第二象限,∴x0<0,
解得x0=-1.∴N(-1,a).
∴直线l的方程为y=-2ax-a…(8分)
代入椭圆方程整理得(1+8a2)x2+8a2x+2a2-2=0.
设A(x1,y1),B(x2,y2).
∴x1+x2=-$\frac{8{a}^{2}}{1+8{a}^{2}}$,x1x2=$\frac{2{a}^{2}-2}{1+8{a}^{2}}$…(10分)
由$\overrightarrow{AD}$=λ$\overrightarrow{AN}$,$\overrightarrow{BD}$=μ$\overrightarrow{BN}$,
得λ=$\frac{{x}_{1}}{1+{x}_{1}}$,μ=$\frac{{x}_{2}}{1+{x}_{2}}$
∴λ+μ=$\frac{{x}_{1}}{1+{x}_{1}}$+$\frac{{x}_{2}}{1+{x}_{2}}$=$\frac{-4-4{a}^{2}}{2{a}^{2}-1}$=-4,
∵a>0,
∴a=$\sqrt{2}$
∴抛物线的标准方程为x2=$\frac{\sqrt{2}}{2}$y…(13分)
点评 本题综合考查了椭圆的标准方程及其性质、直线与椭圆相交问题转化为根与系数的关系、直线与抛物线相切问题、导数的几何意义、向量的运算等基础知识与基本技能,考查了推理能力和计算能力.

| A. | 可以做出这样的三角形,且最大内角为$\frac{5π}{6}$ | |
| B. | 可以做出这样的三角形,且最大内角为$\frac{3π}{4}$ | |
| C. | 可以做出这样的三角形,且最大内角为$\frac{2π}{3}$ | |
| D. | 不可能做出这样的三角形 |
| A. | $\frac{{\sqrt{5}}}{8}$ | B. | $\frac{{\sqrt{5}}}{6}$ | C. | $\frac{{\sqrt{5}}}{3}$ | D. | $\frac{{\sqrt{5}}}{4}$ |
| A. | [${\frac{{\sqrt{3}}}{2}$,1) | B. | [$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$) | C. | [$\frac{1}{2}$,1) | D. | [$\frac{\sqrt{2}}{2}$,$\frac{\sqrt{3}}{2}$] |
| A. | 1 | B. | 2 | C. | $\frac{1}{e}$ | D. | e |
| A. | $\frac{2}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{{2\sqrt{5}}}{5}$ | D. | $\frac{{4\sqrt{5}}}{5}$ |
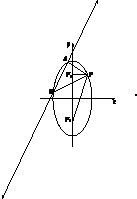 已知F1,F2是椭圆$\frac{y^2}{4}+\frac{x^2}{2}$=1的两焦点,P是椭圆在第一象限弧上一点,且满足$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}$=1,直线l:y=$\sqrt{2}$x+m与椭圆交于A,B两点.
已知F1,F2是椭圆$\frac{y^2}{4}+\frac{x^2}{2}$=1的两焦点,P是椭圆在第一象限弧上一点,且满足$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}$=1,直线l:y=$\sqrt{2}$x+m与椭圆交于A,B两点.