题目内容
3．方程lgx-4+x=0的根一定位于区间（ ）| A． | （5，6） | B． | （3，4） | C． | （2，3） | D． | （1，2） |
分析 先由lgx-4+x=0得：lgx=4-x，再将方程lgx-4+x=0的解的问题转化为函数图象的交点问题解决，先分别画出方程左右两边相应的函数的图象，观察两个函数图象交点的横坐标所在的区间即可．
解答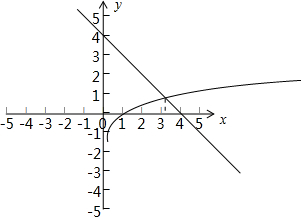 
解：由lgx-4+x=0得：lgx=4-x．
分别画出等式：lgx=4-x两边对应的函数图象：如图．
由图知：它们的交点x0在区间（3，4）内，
故选：B．
点评 本小题主要考查对数函数的图象，考查运算求解能力，考查数形结合思想、化归与转化思想．对数函数的图象是对数函数的一种表达形式，形象地显示了函数的性质，为研究它的数量关系提供了“形”的直观性．属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
5．将正整数1，2，3，4，5随机分成甲乙两组，使得每组至少有一个数，则每组中各数之和是3的倍数的概率是（ ）
| A． | $\frac{2}{21}$ | B． | $\frac{1}{3}$ | C． | $\frac{2}{3}$ | D． | $\frac{2}{5}$ |
6．已知P（B）＞0，A1A2=∅，则下列式子成立的是（ ）
①P（A1|B）＞0②P（A1∪A2|B）=P（A1|B）+P（A2|B）③P（A1$\overrightarrow{{A}_{2}}$|B）≠0④P（$\overline{{A}_{1}{A}_{2}}$|B）=1．
①P（A1|B）＞0②P（A1∪A2|B）=P（A1|B）+P（A2|B）③P（A1$\overrightarrow{{A}_{2}}$|B）≠0④P（$\overline{{A}_{1}{A}_{2}}$|B）=1．
| A． | ①②③④ | B． | ② | C． | ②③ | D． | ②④ |
11．椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1（a＞b＞0）的两个焦点F1，F2，点M在椭圆上，且MF1⊥F1F2，|MF1|=$\frac{4}{3}$，|MF2|=$\frac{14}{3}$，则离心率e等于（ ）
| A． | $\frac{{\sqrt{5}}}{8}$ | B． | $\frac{{\sqrt{5}}}{6}$ | C． | $\frac{{\sqrt{5}}}{3}$ | D． | $\frac{{\sqrt{5}}}{4}$ |
已知F1，F2是椭圆$\frac{y^2}{4}+\frac{x^2}{2}$=1的两焦点，P是椭圆在第一象限弧上一点，且满足$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}$=1，直线l：y=$\sqrt{2}$x+m与椭圆交于A，B两点．
12．曲线y=lnx在点A（e，1）处的切线斜率为 （ ）
| A． | 1 | B． | 2 | C． | $\frac{1}{e}$ | D． | e |
如图，F是抛物线E：y2=2px（p＞0）的焦点，A是抛物线E上任意一点．现给出下列四个结论：