题目内容
【题目】已知抛物线y2=2px（p＞0）的准线为l，若l与圆x2+y2+6x+5=0的交点为A，B，且|AB|=2 
．则p的值为 ．
【答案】4或8
【解析】解：抛物线y2=2px的焦点F（ 
，0），准线x=﹣ ，准线与x轴相交于H， 圆x2+y2+6x+5=0的标准方程（x+3）2+y2=4，则圆心E（﹣3，0），半径为2，
假设抛物线的准线在圆心的左侧，
由丨AB丨=2 
，则A（﹣ ， ），则丨AH丨= ，丨AE丨=2
丨EH丨=1，则丨EH丨+ =丨OE丨，即1+ =3，则p=4，
设抛物线的准线在圆心的右侧，由丨AB丨=2 ，则A（﹣ ， ），则丨AH丨= ，丨AE丨=2
则丨OE丨+丨EH丨= ，即3+1= ，则p=8，
∴p的值为4或8．
所以答案是：4或8．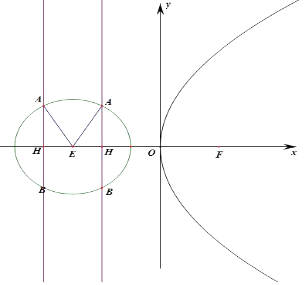
练习册系列答案
相关题目
【题目】某工厂生产甲、乙两种产品.已知生产一吨甲产品、一吨乙产品所需要的煤、电以及产值如表所示；又知道国家每天分配给该厂的煤和电力有限制，每天供煤至多56吨，供电至多45千瓦.问该厂如何安排生产，才能使该厂日产值最大？最大的产值是多少？
用煤（吨） | 用电（千瓦） | 产值（万元） | |
生产一吨 甲种产品 | 7 | 2 | 8 |
生产一吨 乙种产品 | 3 | 5 | 11 |
