题目内容
【题目】设函数![]()
(1)当![]() ,
, ![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
(2)设![]() 在
在![]() 上有两个极值点
上有两个极值点![]() .
.
(A)求实数![]() 的取值范围;
的取值范围;
(B)求证: ![]() .
.
【答案】(1)![]() ;(2)(A)
;(2)(A)![]() ;(B)证明见解析;
;(B)证明见解析;
【解析】试题分析:(1)构造函数![]() ,求导数分
,求导数分![]() ,
, ![]() ,
, ![]() ,
, ![]() 出函数的最值即可,
出函数的最值即可,
(2)函数![]() 有两个极值点
有两个极值点![]() 、
、![]() ,即导函数g′(x)有两个不同的实数根,对a进行分类讨论,不妨设
,即导函数g′(x)有两个不同的实数根,对a进行分类讨论,不妨设![]() ,则
,则![]() ,构造函数
,构造函数![]() ,
, ![]() .,利用函数
.,利用函数![]() 的单调性证明不等式.
的单调性证明不等式.
试题解析:
解:(1)∵![]() ,且
,且![]() ,
,
∴![]() .
.
令![]() ,则
,则![]() .
.
①当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上为单调递增函数,
上为单调递增函数,
∴![]() 时,
时, ![]() ,不合题意.
,不合题意.
②当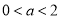 时,
时, ![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上为单调递增函数,
上为单调递增函数,
∴![]() ,
, ![]() ,不合题意.
,不合题意.
③当![]() 时,
时, ![]() ,
, ![]() ,
, ![]() 在
在![]() 上为单调递减函数.
上为单调递减函数.
∴![]() 时,
时, ![]() ,不合题意.
,不合题意.
④当![]() 时,
时, ![]() ,
, ![]() ,
, ![]() 在
在![]() 上为单调递增函数.
上为单调递增函数.
![]() ,
, ![]() ,
, ![]() 在
在![]() 上为单调递减函数.
上为单调递减函数.
∴![]() ,符合题意.
,符合题意.
综上, ![]() .
.
(2)![]() ,
, ![]() .
.
![]() .
.
令![]() ,则
,则![]()
由已知![]() 在
在![]() 上有两个不等的实根.
上有两个不等的实根.
(A)①当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上为单调递增函数,不合题意.
上为单调递增函数,不合题意.
②当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上为单调递减函数,不合题意.
上为单调递减函数,不合题意.
③当![]() 时,
时, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
所以, ![]() ,
, ![]() ,
, ![]() ,解得
,解得![]() .
.
(B)由已知![]() ,
, ![]() ,
,
∴![]() .
.
不妨设![]() ,则
,则![]() ,则
,则![]()
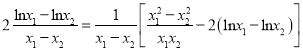
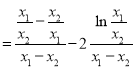 .
.
令![]() ,
, ![]() .
.
则![]() ,∴
,∴![]() 在
在![]() 上为单调递增函数,
上为单调递增函数,
∴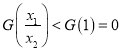
即![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
由(A)![]() ,
,
∴![]() ,
, ![]() ,
,
∴![]() .
.

练习册系列答案
相关题目
【题目】某个服装店经营某种服装,在某周内获纯利润y/元与该周每天销售这种服装件数x/件之间的数据如表:
X | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
y | 66 | 69 | 73 | 81 | 89 | 90 | 91 |
已知x12+x22+…+x72=280,x1y1+x2y2+…+x7y7=3487.
(1)求 ![]() ,
, ![]() ;
;
(2)画出散点图;
(3)判断纯利润y与每天销售件数x之间是否线性相关,如果线性相关,求出线性回归方程.