题目内容
15．
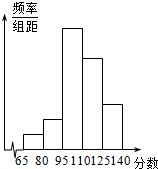为了解某校高二学生联考数学成绩分布，从该校参加联科的学生数学成绩中抽取一个样本，并分成5组，绘成如图所示的频率分布直方图，若第一组至第五组数据的频率之比为1：2：8：6：3，最后一组数据的频率是6，则样本容量为40；众数为102.5．
分析 根据频率=$\frac{频数}{样本容量}$以及频率分布直方图，求出对应的值即可．
解答 解：该校高二学生数学成绩最后一组的概率为
$\frac{3}{1+2+8+6+3}$=0.15，
∴样本容量为
m=$\frac{6}{0.15}$=40；
又根据频率分布直方图，得
众数应在95～110的中点处，
为$\frac{95+110}{2}$=102.5．
故答案为：40，102.5．
点评 本题考查了频率分布直方图的应用问题，也考查了众数的概念与应用问题，是基础题目．
练习册系列答案
阅读快车系列答案
相关题目
10．若P是两条异面直线l、m外的任意一点，则过点P有且只有一条直线与l、m都（ ）
| A． | 平行 | B． | 异面 | C． | 相交 | D． | 垂直 |
20．已知随机变量服从二项分布B（n，p），若E（x）=30，D（x）=20，则p=（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{6}$ | D． | $\frac{1}{9}$ |
7．在等比数列{an}中，a3=4a1，则公比q的值为（ ）
| A． | 1 | B． | 2 | C． | 4 | D． | 8 |
4．
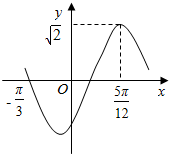函数f（x）=$\sqrt{2}$sin（ωx+θ）（x∈R，ω＞0，|θ|＜$\frac{π}{2}$）的部分图象如图所示，则f（x）的单调递减区间为（ ）
函数f（x）=$\sqrt{2}$sin（ωx+θ）（x∈R，ω＞0，|θ|＜$\frac{π}{2}$）的部分图象如图所示，则f（x）的单调递减区间为（ ）| A． | $[\frac{5π}{12}+kπ，\frac{11π}{12}+kπ]，k∈z$ | B． | $[\frac{5π}{6}+kπ≤x≤\frac{11π}{6}+kπ]，k∈z$ | ||
| C． | $[\frac{5π}{12}+2kπ，\frac{11π}{12}+2kπ]，k∈z$ | D． | $[-\frac{π}{12}+kπ，\frac{5π}{12}+kπ]，k∈z$ |