题目内容
2. 浑南“万达广场”五一期间举办“万达杯”游戏大赛.每5人组成一队,编号为1,2,3,4,5,在其中的投掷飞镖比赛中,要求随机抽取3名队员参加,每人投掷一次.假设飞镖每次都能投中靶面,且靶面上每点被投中的可能性相同.某人投中靶面内阴影区域记为“成功”(靶面为圆形,ABCD为正方形).每队至少有2人“成功”则可获得奖品(其中任何两位队员“成功”与否互不影响).
浑南“万达广场”五一期间举办“万达杯”游戏大赛.每5人组成一队,编号为1,2,3,4,5,在其中的投掷飞镖比赛中,要求随机抽取3名队员参加,每人投掷一次.假设飞镖每次都能投中靶面,且靶面上每点被投中的可能性相同.某人投中靶面内阴影区域记为“成功”(靶面为圆形,ABCD为正方形).每队至少有2人“成功”则可获得奖品(其中任何两位队员“成功”与否互不影响).(Ⅰ)某队中有3男2女,求事件A:“参加投掷飞镖比赛的3人中有男有女”的概率;
(Ⅱ)求某队可获得奖品的概率.
分析 (I)假设某队中1,2,3号为男性,4,5号为女性,在从5人中列出抽取3人的所有可能情况,其中事件$\bar A$包括(1,2,3)一种情况,然后求解参加投掷飞镖比赛的3人中有男有女”的概率.
(II)设事件Ai表示第i个人成功,求出$P({A_i})=\frac{{\frac{1}{2}π{{(OM)}^2}}}{{π{{(OD)}^2}}}=\frac{1}{4}$,(i=1,2,3),设事件B表示某队可获得奖品,即至少有2人“成功”求出P(B),即可得到结果.
解答 解:(I)假设某队中1,2,3号为男性,4,5号为女性,在从5人中
抽取3人的所有可能情况有(1,2,3)(1,2,4)(1,2,5)(1,3,4)
(1,3,5)(1,4,5)(2,3,4)(2,3,5)(2,4,5)(3,4,5)共10个基本事件
其中事件$\bar A$包括(1,2,3)一种情况,
∴$P(A)=1=P(\bar A)=1-\frac{1}{10}=\frac{9}{10}$
答:“参加投掷飞镖比赛的3人中有男有女”的概率为$\frac{9}{10}$…(6分)
(II)由图可知$OD=\sqrt{2}OM$,
设事件Ai表示第i个人成功,则$P({A_i})=\frac{{\frac{1}{2}π{{(OM)}^2}}}{{π{{(OD)}^2}}}=\frac{1}{4}$,(i=1,2,3)
设事件B表示某队可获得奖品,即至少有2人“成功”
则$P(B)=P({A_1}∩{A_2}∩{A_3})+P(\overline{A_1}∩{A_2}∩{A_3})+P({A_1}∩\overline{A_2}∩{A_3})+P({A_1}∩{A_2}∩\overline{A_3})$=$\frac{1}{4}×\frac{1}{4}×\frac{1}{4}+\frac{3}{4}×\frac{1}{4}×\frac{1}{4}+\frac{1}{4}×\frac{3}{4}×\frac{1}{4}+\frac{1}{4}×\frac{1}{4}×\frac{3}{4}$=$\frac{5}{32}$,
答:某队可获得奖品的概率为$\frac{5}{32}$.
点评 本题考查古典概型概率的求法,对立事件的概率的求法,考查计算能力.


| A. | 4$\sqrt{3}$π | B. | $\frac{4\sqrt{3}π}{3}$ | C. | 4$\sqrt{2}$π | D. | $\frac{4\sqrt{2}π}{3}$ |
| A. | -$\frac{7}{4}$ | B. | -$\frac{5}{4}$ | C. | -$\frac{3}{4}$ | D. | -$\frac{1}{4}$ |
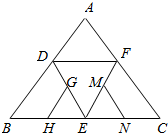 如图是正四面体的平面展开图,G、H、M、N分别为DE、BE、EF、EC的中点,在这个正四面体中,
如图是正四面体的平面展开图,G、H、M、N分别为DE、BE、EF、EC的中点,在这个正四面体中,