题目内容
3. 如图所示是三棱锥D-ABC的三视图,若在三棱锥的直观图中,点O为线段BC的中点,则异面直线DO与AB所成角的余弦值等于$\frac{\sqrt{6}}{6}$.
如图所示是三棱锥D-ABC的三视图,若在三棱锥的直观图中,点O为线段BC的中点,则异面直线DO与AB所成角的余弦值等于$\frac{\sqrt{6}}{6}$.
分析 根据三视图可得AB=AC=2,BD=2,AB⊥AC,BC=2$\sqrt{2}$,AB⊥平面ABC.取AC的中点E,则∠DOE或其补角,即为异面直线DO与AB所成角.△DOE中,由余弦定理求得cos∠DOE 的值,可得结论.
解答 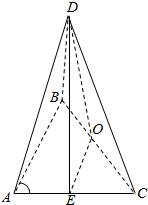 解:如图所示:根据三视图可得AB=AC=2,BD=2,AB⊥AC,BC=$\sqrt{{AB}^{2}{+AC}^{2}}$=2$\sqrt{2}$,AB⊥平面ABC.
解:如图所示:根据三视图可得AB=AC=2,BD=2,AB⊥AC,BC=$\sqrt{{AB}^{2}{+AC}^{2}}$=2$\sqrt{2}$,AB⊥平面ABC.
取AC的中点E,则由O为BC的中点可得OE=$\frac{1}{2}$AB=1,OE∥AB,∴∠DOE或其补角,即为异面直线DO与AB所成角.
又DO=$\sqrt{{BD}^{2}{+BO}^{2}}$=$\sqrt{4+2}$=$\sqrt{6}$,DE=$\sqrt{{BD}^{2}{+BE}^{2}}$=$\sqrt{4+(4+1)}$=3,
△DOE中,由余弦定理可得cos∠DOE=$\frac{{DO}^{2}{+OE}^{2}{-DE}^{2}}{2DO•OE}$=$\frac{6+1-9}{2\sqrt{6}×1}$=-$\frac{\sqrt{6}}{6}$,
∴异面直线DO与AB所成角的余弦值等于$\frac{\sqrt{6}}{6}$,
故答案为:$\frac{\sqrt{6}}{6}$.
点评 本题主要考查几何体的三视图,异面直线所成的角的定义和求法,余弦定理,体现了转化、数形结合的数学思想,属于中档题.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案
相关题目
13.某几何体的三视图如图所示,则该几何体的外接球的体积为( )


| A. | 4$\sqrt{3}$π | B. | $\frac{4\sqrt{3}π}{3}$ | C. | 4$\sqrt{2}$π | D. | $\frac{4\sqrt{2}π}{3}$ |
18.( 1+i)10的展开式中,系数最大的项是( )
| A. | 第5项 | B. | 第6项 | C. | 第7项 | D. | 第5项或第6项 |
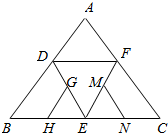 如图是正四面体的平面展开图,G、H、M、N分别为DE、BE、EF、EC的中点,在这个正四面体中,
如图是正四面体的平面展开图,G、H、M、N分别为DE、BE、EF、EC的中点,在这个正四面体中,