题目内容
8．化简：（1）（2a${\;}^{\frac{1}{4}}$b${\;}^{\frac{1}{3}}$）（-3a${\;}^{-\frac{1}{2}}$b${\;}^{\frac{2}{3}}$）÷（-$\frac{1}{4}$a${\;}^{-\frac{1}{4}}$b${\;}^{-\frac{2}{3}}$）；
（2）log225•log3$\frac{1}{16}$•log5$\frac{1}{9}$．
分析 （1）根据指数幂的运算性质计算即可；
（2）利用换底公式和对数的运算性质计算即可．
解答 解：（1）（2a${\;}^{\frac{1}{4}}$b${\;}^{\frac{1}{3}}$）（-3a${\;}^{-\frac{1}{2}}$b${\;}^{\frac{2}{3}}$）÷（-$\frac{1}{4}$a${\;}^{-\frac{1}{4}}$b${\;}^{-\frac{2}{3}}$）=2×（-3）×（-4）${a}^{\frac{1}{4}-\frac{1}{2}+\frac{1}{4}}$${b}^{\frac{1}{3}+\frac{2}{3}+\frac{2}{3}}$=24${b}^{\frac{5}{3}}$
（2）原式=log252•log32-4•log53-2
=$\frac{2lg5}{lg2}$•$\frac{-4lg2}{lg3}$•$\frac{-2lg3}{lg5}$=16．
点评 本题考查了指数幂的运算性质和对数的运算性质，以及换底公式，属于基础题．
练习册系列答案
相关题目
3．i为虚数单位，则$|{\frac{1+i}{i}}|$等于（ ）
| A． | 1-i | B． | 1+i | C． | $\sqrt{2}$ | D． | 2 |
16．已知椭圆C的中心在原点，左焦点F1，右焦点F2均在x轴上，A为椭圆的右顶点，B为椭圆短轴的端点，P是椭圆上一点，且PF1⊥x轴，PF2∥AB，则此椭圆的离心率等于（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{{\sqrt{2}}}{2}$ | C． | $\frac{1}{3}$ | D． | $\frac{{\sqrt{5}}}{5}$ |
3．设a=（$\frac{3}{4}$）${\;}^{-\frac{1}{3}}$，b=（$\frac{4}{3}$）${\;}^{\frac{1}{4}}$，c=（$\frac{3}{2}$）${\;}^{-\frac{3}{4}}$，则a，b，c的大小顺序为（ ）
| A． | c＜b＜a | B． | c＜a＜b | C． | b＜c＜a | D． | b＜a＜c |
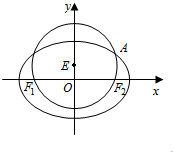已知圆E：x2+（y-$\frac{1}{2}$）2=$\frac{9}{4}$经过椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左右焦点F1，F2，且与椭圆C在第一象限的交点为A，且F1，E，A三点共线，直线l交椭圆C于M，N两点，且$\overrightarrow{MN}$=λ$\overrightarrow{OA}$（λ≠0）
20．已知数列{an}，点{n，an}在函数$f（x）=sin（πx+\frac{π}{3}）$的图象上，则a2015的值为（ ）
| A． | $\frac{{\sqrt{3}}}{2}$ | B． | $-\frac{{\sqrt{3}}}{2}$ | C． | $\frac{1}{2}$ | D． | $-\frac{1}{2}$ |