题目内容
【题目】随着手机使用的不断普及,现在全国各地的中小学生携带手机进入校园已经成为了普遍的现象,也引起了一系列的问题。然而,是堵还是疏,就摆在了我们学校老师的面前.某研究型学习小组调查研究“中学生使用手机对学习的影响”,部分统计数据如下表:
不使用手机 | 使用手机 | 合计 | |
学习成绩优秀人数 | 18 | 7 | 25 |
学习成绩不优秀人数 | 6 | 19 | 25 |
合计 | 24 | 26 | 50 |
参考数据:![]() ,其中
,其中![]() .
.
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(1)试根据以上数据,运用独立性检验思想,指出有多大把握认为中学生使用手机对学习有影响?
(2)研究小组将该样本中使用手机且成绩优秀的7位同学记为![]() 组,不使用手机且成绩优秀的18位同学记为
组,不使用手机且成绩优秀的18位同学记为![]() 组,计划从
组,计划从![]() 组推选的2人和
组推选的2人和![]() 组推选的3人中,随机挑选两人来分享学习经验.求挑选的两人中一人来自
组推选的3人中,随机挑选两人来分享学习经验.求挑选的两人中一人来自![]() 组、另一人来自
组、另一人来自![]() 组的概率.
组的概率.
【答案】见解析
【解析】(1)根据上方公式求得![]() ,
,
所以该研究小组有![]() 的把握认为中学生使用手机对学习有影响.……………………5分
的把握认为中学生使用手机对学习有影响.……………………5分
(2)记![]() 组推选的两名同学分别为
组推选的两名同学分别为![]() ,
,![]() 组推选的三名同学分别为
组推选的三名同学分别为![]() ,则从这
,则从这![]() 人中任取两人有
人中任取两人有![]() , 共
, 共![]() 种取法,其中一人来自
种取法,其中一人来自![]() 组、另一人来自
组、另一人来自![]() 组有
组有![]() 种取法,故挑选的两人中一人来自
种取法,故挑选的两人中一人来自![]() 组、另一人来自
组、另一人来自![]() 组的概率为
组的概率为![]() .………12分
.………12分
【命题意图】本题主要考查古典概型及其概率的计算;独立性检验等基础知识,以及考查识图能力、审读能力、获取信息的能力、分类讨论思想.

 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案【题目】某地区2007年至2013年农村居民家庭纯收入y(单位:千元)的数据如下表:
年份 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(1)求y关于t的线性回归方程;
(2)利用(1)中的回归方程,分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2015年农村居民家庭人均纯收入.
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
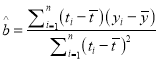 ,
, ![]()
【题目】某品牌手机厂商推出新款的旗舰机型,并在某地区跟踪调查得到这款手机上市时间(第x周)和市场占有率(y﹪)的几组相关数据如下表:
| 1 | 2 | 3 | 4 | 5 |
| 0.03 | 0.06 | 0.1 | 0.14 | 0.17 |
(Ⅰ)根据表中的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(Ⅱ)根据上述线性回归方程,分析该款旗舰机型市场占有率的变化趋势,并预测在第几周,该款旗舰机型市场占有率将首次超过 0.40﹪(最后结果精确到整数).
参考公式: ,
,![]()

