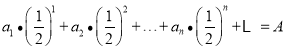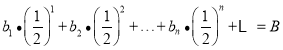题目内容
【题目】已知函数f(x)＝lg(1－x)＋lg(1＋x)＋x4－2x2.
(1)求函数f(x)的定义域；
(2)判断函数f(x)的奇偶性；
(3)求函数f(x)的值域．
【答案】（1）(－1，1)（2）f(x)是偶函数（3）(－∞，0]
【解析】
(1)由
得－1<x<1，所以函数f(x)的定义域为(－1，1)．
(2)由f(－x)＝lg(1＋x)＋lg(1－x)＋(－x)4－2(－x)2＝lg(1－x)＋lg(1＋x)＋x4－2x2＝f(x)，
所以函数f(x)是偶函数．
(3)f(x)＝lg(1－x)＋lg(1＋x)＋x4－2x2＝lg(1－x2)＋x4－2x2，
设t＝1－x2，由x∈(－1，1)，得t∈(0，1]．
所以y＝lg(1－x2)＋x4－2x2＝lgt＋(t2－1)，t∈(0，1]，
设0<t1<t2≤1，则lgt1<lgt2，
<
，
所以lgt1＋(－1)<lgt2＋(－1)，
所以函数y＝lgt＋(t2－1)在t∈(0，1]上为增函数，
所以函数f(x)的值域为(－∞，0]．
练习册系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
