题目内容
【题目】已知函数f(x)=x3-3ax-1,a≠0.
(1)求f(x)的单调区间;
(2)若f(x)在x=-1处取得极值,直线y=m与y=f(x)的图象有三个不同的交点,求m的取值范围.
【答案】见解析
【解析】(1)f′(x)=3x2-3a=3(x2-a),
当a<0时,对x∈R,有f′(x)>0,
∴当a<0时,f(x)的单调增区间为(-∞,+∞);
当a>0时,由f′(x)>0,解得x<-![]() 或x>
或x>![]() ,
,
由f′(x)<0,解得-![]() <x<
<x<![]() ,
,
∴当a>0时,f(x)的单调增区间为(-∞,-![]() ),(
),(![]() ,+∞);单调减区间为(-
,+∞);单调减区间为(-![]() ,
,![]() ).
).
(2)∵f(x)在x=-1处取得极值,
∴f′(-1)=3×(-1)2-3a=0,∴a=1.
∴f(x)=x3-3x-1,
f′(x)=3x2-3,
由f′(x)=0,
解得x1=-1,x2=1.
由(1)中f(x)的单调性可知,f(x)在x=-1处取得极大值f(-1)=1,在x=1处取得极小值f(1)=-3.
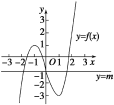
因为直线y=m与函数y=f(x)的图象有三个不同的交点,
结合如图所示f(x)的图象可知:
m的取值范围是(-3,1).

练习册系列答案
相关题目