题目内容
【题目】用长为
，宽为
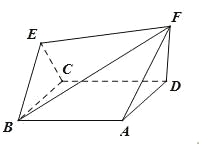
的长方形铁皮做一个无盖的容器.先在四角分别截去一个小正方形，然后把四边翻转
，再焊接而成（如图）.问该容器的高为多少时，容器的容积最大？最大容积是多少？
【答案】当容器高为10cm时，最大容积是19600cm2
【解析】试题分析：首先分析题目求长为90cm，宽为48cm的长方形铁皮做一个无盖的容器当容器的高为多少时，容器的容积最大．故可设容器的高为x，体积为V，求出v关于x的方程，然后求出导函数，分析单调性即可求得最值．
解：根据题意可设容器的高为x，容器的体积为V，
则有V=（90﹣2x）（48﹣2x）x=4x3﹣276x2+4320x，（0＜x＜24）
求导可得到：V′=12x2﹣552x+4320
由V′=12x2﹣552x+4320=0得x1=10，x2=36．
所以当x＜10时，V′＞0，
当10＜x＜36时，V′＜0，
当x＞36时，V′＞0，
所以，当x=10，V有极大值V（10）=19600，又V（0）=0，V（24）=0，
所以当x=10，V有最大值V（10）=19600
故答案为当高为10，最大容积为19600．
【题目】某高校共有学生15000人，其中男生10500人，女生4500人，为调查该校学生每周平均体育运动时间的情况，采用分层抽样的方法，收集300位学生每周平均体育运动时间的样本数据（单位：小时）．
（1）应收集多少位女生的样本数据？
（2）根据这300样本数据，得到学生每周平均体育运动时间的频率分布直方图（如图所示），其中样本数据的分组区间为： 
．估计该校学生每周平均体育运动时间超过4小时的概率；
（3）在样本数据中，有60位女生的每周平均体育运动时间超过4小时，请完成每周平均体育运动时间与性别的列联表，并判断是否有95%的把握认为“该校学生的每周平均体育运动时间与性别有关”．
| 0.10 | 0.05 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |
附： 
【题目】东亚运动会将于2013年10月6日在天津举行．为了搞好接待工作，组委会打算学习北京奥运会招募大量志愿者的经验，在某学院招募了16名男志愿者和14名女志愿者，调查发现，男女志愿者中分别有10人和6人喜爱运动，其余人不喜欢运动．
(1)根据以上数据完成以下2×2列联表：
喜爱运动 | 不喜爱运动 | 总计 | |
男 | 10 | 16 | |
女 | 6 | 14 | |
总计 | 30 |
(2)根据列联表的独立性检验，能否在犯错误的概率不超过0.10的前提下认为性别与喜爱运动有关？
(3)如果从喜欢运动的女志愿者中(其中恰有4人会外语)，抽取2名负责翻译工作，那么抽出的志愿者中至少有1人能胜任翻译工作的概率是多少？
参考公式：K2＝
，其中
n＝a＋b＋c＋d.
参考数据：
P(K2≥k) | 0.40 | 0.25 | 0.10 | 0.010 |
k | 0.708 | 1.323 | 2.706 | 6.635 |