题目内容
14.用柯西不等式比较a3+b3+c3与a2b+b2c+c2a 的大小.分析 设a≥b≥c,则a2≥b2≥c2,两式相乘,正序大于乱序,可得结论.
解答 证明:设a≥b≥c,则a2≥b2≥c2,
∮两式相乘,正序大于乱序,则有a3+b3+c3≥a2b+b2c+c2a.
点评 本题考查排序不等式,考查学生分析解决问题的能力,比较基础.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
5.已知全集U=R,M={x|x2<2x},则∁UM=( )
| A. | {x|X≥2} | B. | {x|x>2} | C. | {x|x≤0或x≥2} | D. | {x|0<x<2} |
2.若a>0且a≠1,函数y=ax-3+1的反函数图象一定过点A,则A的坐标是( )
| A. | (1,0) | B. | (0,1) | C. | (2,3) | D. | (3,2) |
7.设i是虚数单位,若z=cosθ+isinθ且对应的点位于复平面的第二象限,则θ位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
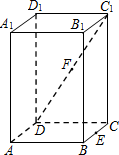 如图,在正四棱柱(底面是正方形的直棱柱)ABCD-A1B1C1D1中,E是BC的中点,F是C1D的中点,P是棱CC1所在直线上的动点.则下列四个命题:
如图,在正四棱柱(底面是正方形的直棱柱)ABCD-A1B1C1D1中,E是BC的中点,F是C1D的中点,P是棱CC1所在直线上的动点.则下列四个命题: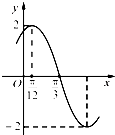 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,下列说法正确的个数是( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,下列说法正确的个数是( )