题目内容
12.若满足条件$\left\{\begin{array}{l}x-y+2≥0\\ x+y-2≥0\\ kx-y-2k+1≥0\end{array}\right.$的点P(x,y)构成三角形区域,则实数k的取值范围是(-∞,-1).分析 作出不等式组对应的平面区域,根据平面区域是三角形,即可确定k的取值范围.
解答 解:作出不等式组对应的平面区域,如图示: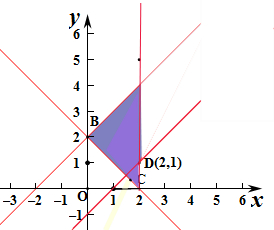
直线kx-y-2k+1=0得k(x-2)+1-y=0,则直线过定点(2,1),
当直线k(x-2)+1-y=0与x+y-2=0平行时,即k=-1时,此时对应的平面区域不是三角形,
∴要使对应的平面区域是三角形,
则k(x-2)+1-y=0与x+y-2=0在第一象限内相交,即k<-1,
故答案为:(-∞,-1).
点评 本题主要考查线性规划的应用,利用数形结合是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.设i是虚数单位,若z=cosθ+isinθ且对应的点位于复平面的第二象限,则θ位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
4.某学生对一些对数进行运算,如图表格所示:
现在发觉学生计算中恰好有两次地方出错,那么出错的数据是( )
| x | 0.21 | 0.27 | 1.5 | 2.8 |
| lgx | 2a+b+c-3(1) | 6a-3b-2(2) | 3a-b+c(3) | 1-2a+2b-c(4) |
| x | 3 | 5 | 6 | 7 |
| lgx | 2a-b(5) | a+c(6) | 1+a-b-c(7) | 2(a+c)(8) |
| x | 8 | 9 | 14 | |
| lgx | 3-3a-3c(9) | 4a-2b(10) | 1-a+2b(11) |
| A. | (3),(8) | B. | (4),(11) | C. | (1),(3) | D. | (1),(4) |
 在如图所示的几何体中,四边形CDEF为正方形,四边形ABCD为等腰梯形,AB∥CD,AC=$\sqrt{3}$,AB=2BC=2,AC⊥FB.
在如图所示的几何体中,四边形CDEF为正方形,四边形ABCD为等腰梯形,AB∥CD,AC=$\sqrt{3}$,AB=2BC=2,AC⊥FB.