题目内容
数列-
,
,-
,
,…的一个通项公式是( )
| 4 |
| 3 |
| 9 |
| 5 |
| 16 |
| 7 |
| 25 |
| 9 |
A、an=(-1)n
| ||
B、an=(-1)n
| ||
C、an=(-1)n
| ||
D、an=(-1)n
|
考点:数列的概念及简单表示法
专题:点列、递归数列与数学归纳法
分析:由数列-
,
,-
,
,….可知:an的符号为(-1)n,其分子为平方数(n+1)2,分母为奇数2n+1.即可得出.
| 4 |
| 3 |
| 9 |
| 5 |
| 16 |
| 7 |
| 25 |
| 9 |
解答:
解:由数列-
,
,-
,
,….
可知:an的符号为(-1)n,其分子为平方数(n+1)2,分母为奇数2n+1.
因此可得一个通项公式为an=(-1)n•
.
故选:D.
| 4 |
| 3 |
| 9 |
| 5 |
| 16 |
| 7 |
| 25 |
| 9 |
可知:an的符号为(-1)n,其分子为平方数(n+1)2,分母为奇数2n+1.
因此可得一个通项公式为an=(-1)n•
| (n+1)2 |
| 2n+1 |
故选:D.
点评:本题考查了通过观察分析归纳得出数列的通项公式,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,四棱锥P-ABCD中,PB⊥底面ABCD,CD⊥PD,底面ABCD为直角梯形,AD∥BC,AB⊥BC,AB=AD=PB=3,点E在棱PA上,且PE=2EA.
如图,四棱锥P-ABCD中,PB⊥底面ABCD,CD⊥PD,底面ABCD为直角梯形,AD∥BC,AB⊥BC,AB=AD=PB=3,点E在棱PA上,且PE=2EA.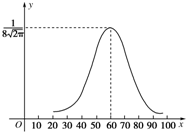 某校1000名学生的某次数学考试成绩X服从正态分布,其密度函数曲线如图,则成绩X位于区间(53,68]的人数大约是
某校1000名学生的某次数学考试成绩X服从正态分布,其密度函数曲线如图,则成绩X位于区间(53,68]的人数大约是