题目内容
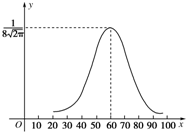 某校1000名学生的某次数学考试成绩X服从正态分布,其密度函数曲线如图,则成绩X位于区间(53,68]的人数大约是
某校1000名学生的某次数学考试成绩X服从正态分布,其密度函数曲线如图,则成绩X位于区间(53,68]的人数大约是考点:正态分布曲线的特点及曲线所表示的意义
专题:综合题,概率与统计
分析:由题图知 X~N(μ,σ2),其中 μ=60,σ=8,P(μ-σ<X≤μ+σ)=P(52<X≤68)=0.682 6,从而得出成绩在(53,68]范围内的学生人数.
解答:
解:由题图知 X~N(μ,σ2),其中 μ=60,σ=8,
∴P(μ-σ<X≤μ+σ)=P(52<X≤68)=0.682 6.
∴人数为 0.682 6×1 000≈682.
故答案为:682.
∴P(μ-σ<X≤μ+σ)=P(52<X≤68)=0.682 6.
∴人数为 0.682 6×1 000≈682.
故答案为:682.
点评:本题考查正态分布曲线的特点及曲线所表示的意义,考查曲线的变化特点,本题是一个基础题.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
数列-
,
,-
,
,…的一个通项公式是( )
| 4 |
| 3 |
| 9 |
| 5 |
| 16 |
| 7 |
| 25 |
| 9 |
A、an=(-1)n
| ||
B、an=(-1)n
| ||
C、an=(-1)n
| ||
D、an=(-1)n
|
已知角α终边上一点A的坐标为(-2,2
),则sinα=( )
| 3 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
下列多项式中能用平方差公式分解因式的是( )
| A、a2+(-b)2 |
| B、5m2-20mn |
| C、-x2-y2 |
| D、-x2+9 |
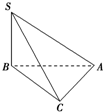 三棱锥S-ABC中,∠SBA=∠SCA=90°,△ABC是斜边AB=a的等腰直角三角形,则以下结论中:
三棱锥S-ABC中,∠SBA=∠SCA=90°,△ABC是斜边AB=a的等腰直角三角形,则以下结论中: